Just as you can add and subtract numbers or polynomial expressions, you can add or subtract functions. Performing operations on functions is in fact just as simple. By keeping a couple of basic concepts in mind, you can quickly learn how to perform function calculations.
Steps
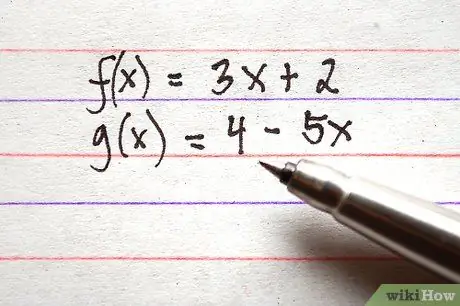
Step 1. Write down all the features you want to add or subtract
Make sure that all terms of functions are on the right side of the equation. As an example, 3 functions in the correct form are listed below.

Step 2. Determine which features you want to add or subtract
Note that the structure of expressions may vary slightly. The sum between f (x) and g (x) can be written as f (x) + g (x) or (f + g) x. The structures of both expressions indicate the same operation.
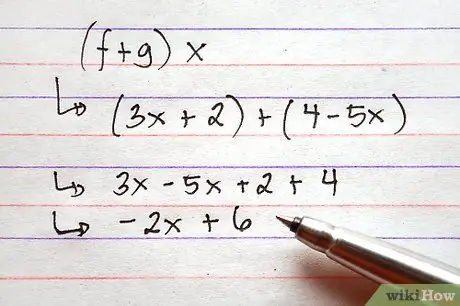
Step 3. Add or subtract functions
To do this, simply add the expressions to the right of the functions by combining all the common terms. This can be done using symbols, which means that it is not necessary to assign values to the terms of the functions before performing the addition.
The image shows two examples using the above functions, an addition problem and a subtraction problem
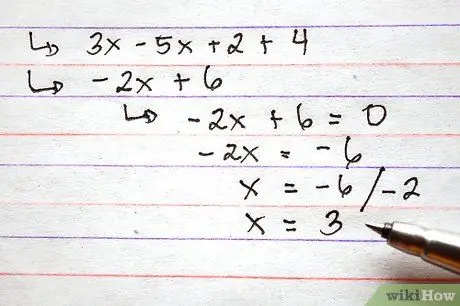
Step 4. Alternatively, assign a value to the functions before performing the addition and subtraction operations
This step can be useful if you are asked to provide the function value for a specific value of x.
- For example, imagine you are asked to solve (f + h) (2). There are two ways to do this. First you could proceed as above and add the equations before substituting the value of x:
- Alternatively, you can substitute the value of x in two equations separately, solve them, and then add the solutions:
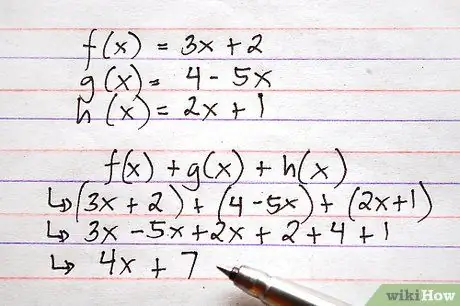
Step 5. Follow the same procedure to add or subtract more than two functions at the same time
Just as it is possible to add or subtract several numbers in the same calculation, it is possible to perform the above operations simultaneously on multiple functions.
Here is an example, using the functions above, which requires both addition and subtraction. Imagine you are asked to calculate f (x) + g (x) + h (x)
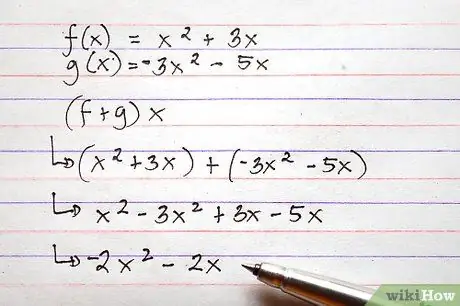
Step 6. Use the same method described above to add and subtract more complex functions
Although the functions involved are much more complex than the examples listed here, the process of addition and subtraction is practically the same.






