A pentagon is a polygon with five sides. Almost all of the mathematical problems you will have to face in your school career study regular pentagons, therefore composed of five identical sides. To calculate the area of this geometric figure there are two methods that will be used on the basis of the information available.
Steps
Method 1 of 3: Calculate the Area From the Length of the Side and the Apothem
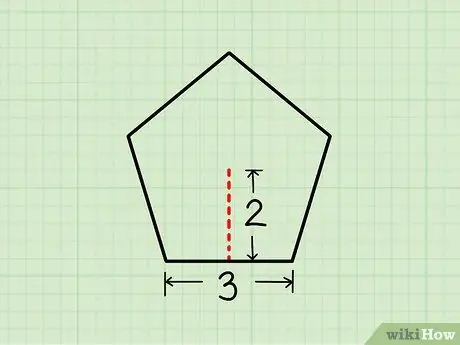
Step 1. Start by measuring the side and the apothem
This method can be applied to regular pentagons, which therefore have 5 identical sides. In addition to knowing the length of the sides, you will also need to know the length of the apothem. By "apothem" of a pentagon we mean the line that, starting from the center of the figure, intersects one side with a right angle of 90 °.
- Do not confuse the apothem with the radius, which in this case is the line that connects the center of the figure with one of the vertices of the pentagon. If the only data you have is side length and radius, use the method described in this section.
-
In this example, a pentagon with long sides is studied
Step 3. unit and apothem lung
Step 2. unit.
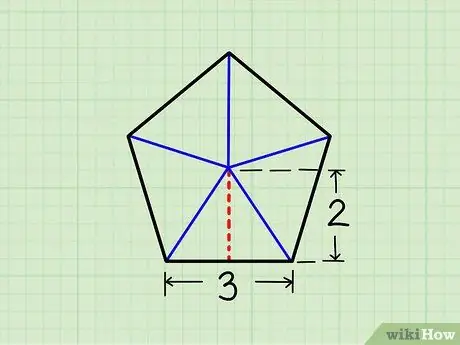
Step 2. Divide the pentagon into five triangles
To do this, draw 5 lines that connect the center of the figure with each of the vertices (the five corners of the figure). At the end you will have obtained five equal triangles.
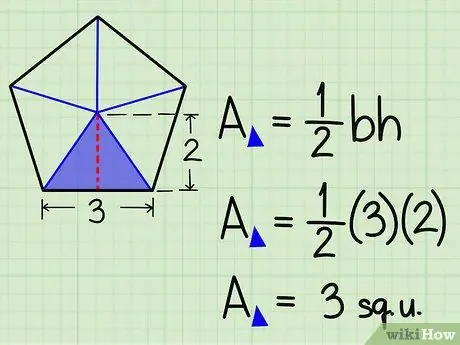
Step 3. Calculate the area of a triangle
Each triangle will have like base one side of the pentagon and how height the apothem (remember that the height of a triangle is the line that joins the vertex and the opposite side creating a right angle). To calculate the area of each triangle you will simply have to use the classic formula: (base x height) / 2.
-
In our example we will get: Area = (3 x 2) / 2 =
Step 3. square units.

Step 4. Multiply the area of a single triangle by 5
Having divided a regular pentagon into five triangles, the latter will all be identical. We therefore deduce that to calculate the total area of the pentagon we simply have to multiply the area of a single triangle by 5.
-
In our example we will get: Area = 5 x (area of the triangle) = 5 x 3 =
Step 15. square units.
Method 2 of 3: Calculate Area From Side Length

Step 1. Start from the length of one side
This method only applies to regular pentagons, i.e. they have 5 identical sides.
-
In this example we are studying a pentagon with long sides
Step 7. unit.
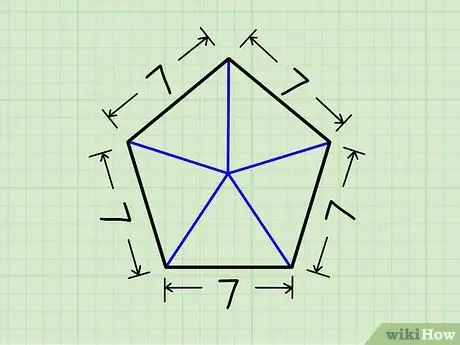
Step 2. Divide the pentagon into 5 triangles
To do this, draw 5 lines that connect the center of the figure with each of the vertices (the 5 corners). At the end you will have obtained 5 equal triangles.

Step 3. Divide a triangle in half
To do this, draw a line that, starting from the center of the pentagon, intersects the base of a triangle forming an angle of 90 °. You will then get two identical right-angled triangles.
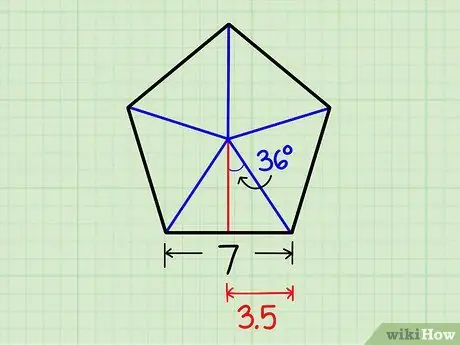
Step 4. Let's study one of the right triangles
We already know a side and an angle of our little triangle, so we can deduce the following:
- There base of our triangle will be equal to half the length of the side of the pentagon. In our example the side measures 7 units, so the base will be equal to 3.5 units.
- The corner at the center of a regular pentagon formed by the radius and the apothem is always 36 ° (starting from the axiom that the round angle is 360 °, dividing the pentagon into 10 right triangles, we will therefore obtain 360 ÷ 10 = 36. So each triangle will have the angle composed of the base and the hypotenuse, with apex in the center of the pentagon, which measures 36 °).
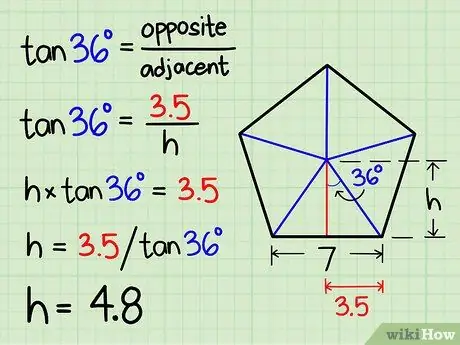
Step 5. Calculate the height of the right triangle. The height of the triangle coincides with the apothem of the pentagon, so it is the line that, starting from the center, intersects the side of the pentagon with an angle of 90 °. To calculate the length of this side we can help ourselves with the basic notions of trigonometry:
- In a right triangle the tangent of one angle is equal to the ratio of the length of the opposite side to the length of the adjacent side.
- The side opposite the 36 ° angle is the base of the triangle (which we know is equal to half the length of the side of the pentagon). The side adjacent to the 36 ° angle is the height of the triangle.
- tan (36º) = opposite side / adjacent side.
- In our example we will therefore obtain: tan (36º) = 3, 5 / height.
- height x tan (36º) = 3, 5
- height = 3, 5 / tan (36º)
- height = 4, 8 units (rounding the result to simplify calculations).
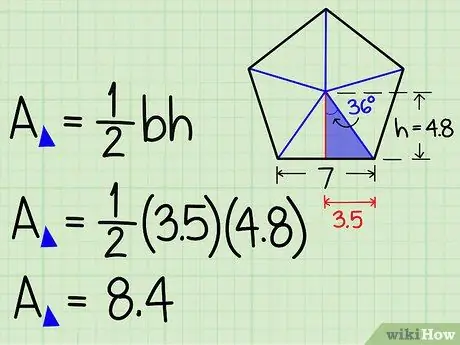
Step 6. We calculate the area of the triangle
The area of a triangle is equal to: (base x height) / 2. Now that we know the height measurement we can use the formula just mentioned to calculate the area of our right triangle.
In our example the area is given by: (base x height) / 2 = (3, 5 x 4, 8) / 2 = 8, 4 square units

Step 7. Multiply the area of a right triangle to get the total area of the pentagon
One of the right-angled triangles we studied covers exactly 1/10 of the total area of the figure in question. So we deduce that to calculate the total area of the pentagon we need to multiply the area of the triangle by 10.
In our example we will then get the following: 8.4 x 10 = 84 square units.
Method 3 of 3: Using the Mathematical Formula

Step 1. Use the perimeter and apothem
By "apothem" of a pentagon we mean the line that, starting from the center of the figure, intersects one side with a right angle of 90 °. If this measure is known, this simple formula can be applied:
- The area of a regular pentagon is equal to: pa / 2, where p is the perimeter and a is the length of the apothem.
- If you don't know the perimeter you can calculate it in the following way starting from the measurement of one side: p = 5s, where s is the length of a single side of the pentagon.
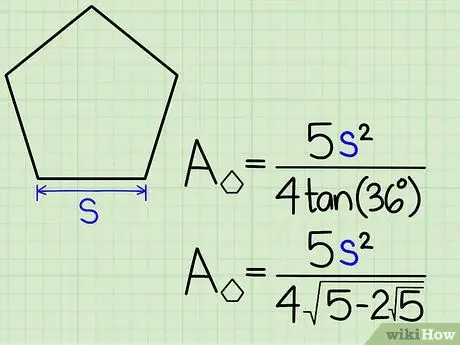
Step 2. Use one side measurement
If you only know the size of a single side you can apply the following formula:
- The area of a regular pentagon is equal to: (5 s 2) / (4tan (36º)), where s is the measure of one side of the figure.
- tan (36º) = √ (5-2√5). If you don't have a calculator that can calculate the tan function of an angle, you can use the following formula: Area = (5 s 2) / (4√(5-2√5)).
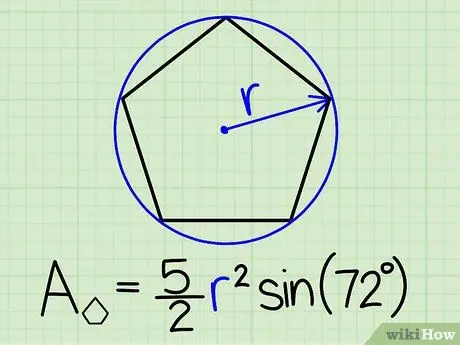
Step 3. Choose the formula that uses only the radius measurement
You can also calculate the area of a regular pentagon starting from the measurement of its radius. The formula is as follows:
The area of a regular pentagon is equal to: (5/2) r 2sin (72º), where r is the measure of the radius.
Advice
- To make the math calculations less complex, rounded values were used in the examples in this article. Calculating the area and other measurements using real data without doing any rounding will give slightly different results.
- If possible, perform the calculations using both the geometric method and the arithmetic formula and compare the results obtained to confirm the correctness of the result. Performing the calculation of the arithmetic formula in a single step (without performing the rounding required by the intermediate steps) you may get a slightly different result, but still very similar to the first. This difference is generated because all the steps that make up the final formula used are not rounded off.
- The study of irregular pentagons (where the sides of the figure are not all the same) is much more complex. Normally the best approach is to divide the irregular pentagon into triangles of which all the areas will be added. Alternatively, you may need to proceed as follows: draw a figure that circumscribes the pentagon, calculate its area and subtract the area not included in the pentagon from it.
- The mathematical formulas are obtained with geometric methods very similar to those described in this article. Try to find out how the formulas used were derived. The formula that uses the radius is much more difficult to deduce than the others (hint: you will have to use the double identity of the angle).






