Area is the measure of the amount of space within a two-dimensional figure. For a solid, we mean the sum of the areas of all the faces from which it is composed. Sometimes, finding the area can simply consist of multiplying two numbers, but it can often be more complicated. Read this article for a brief overview of the following figures: area under an arc of function, surface of prisms and cylinders, circles, triangles and quadrilaterals.
Steps
Method 1 of 10: Rectangles
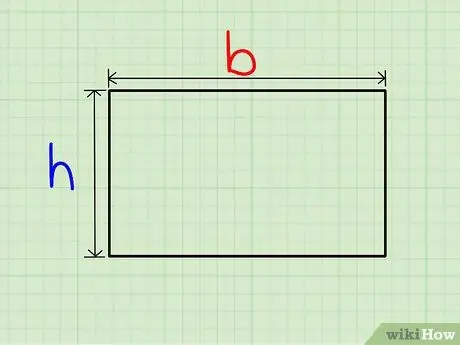
Step 1. Find the lengths of two consecutive sides of the rectangle
Since rectangles have two pairs of sides of equal length, label one side as base (b) and the other as height (h). Generally, the horizontal side is the base and the vertical side is the height.
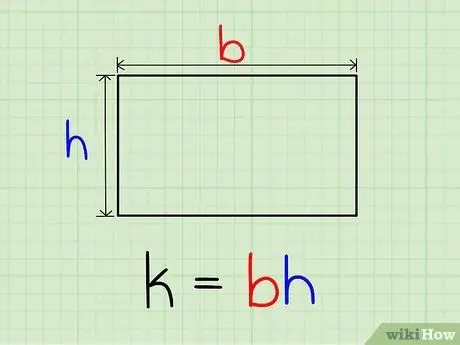
Step 2. Multiply base by height to calculate area
If the area of the rectangle is k, k = b * h. This means that area is simply the product of base and height.
For more in-depth instructions, look for an article on how to find the area of a quadrilateral
Method 2 of 10: Squares
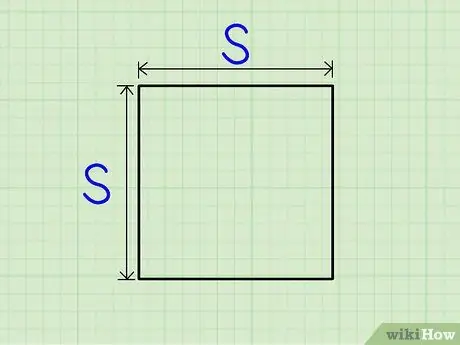
Step 1. Find the length of one side of the square
Having four equal sides, all sides should be this same size.
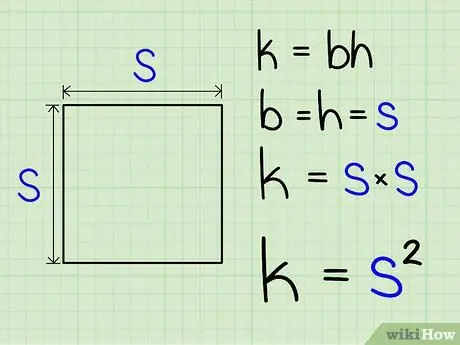
Step 2. Square the length of the side
This is your area.
This works because a square is simply a special rectangle that has equal width and length. Thus, in solving k = b * h, b and h are both the same value. Thus, we end up squaring a single number to find the area
Method 3 of 10: Parallelograms
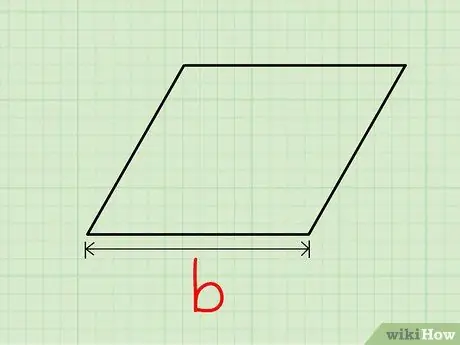
Step 1. Choose a side that is the base of the parallelogram
Find the length of this base.

Step 2. Draw a perpendicular to this base and measure it where it crosses the base and opposite side
This length is the height
If the opposite side of the base isn't long enough to cross the perpendicular line, extend the side until it crosses the perpendicular

Step 3. Enter the base and height into the equation k = b * h
For more specific instructions, read the article on how to find the area of a parallelogram
Method 4 of 10: Trapezes
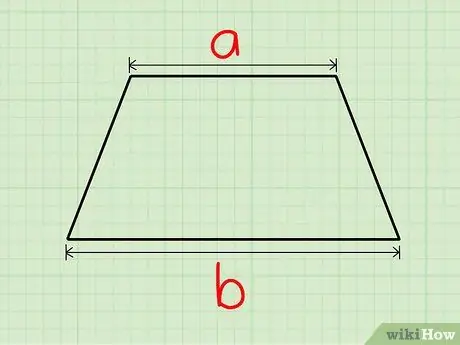
Step 1. Find the lengths of the two parallel sides
Assign these values to variables a and b.
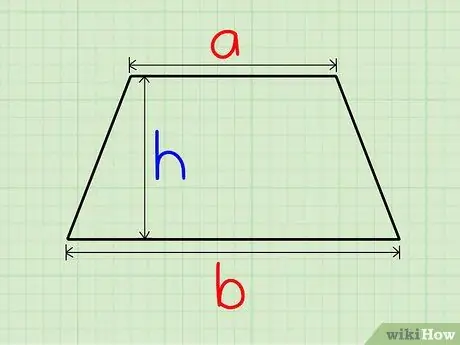
Step 2. Find the height
Draw a perpendicular line that crosses both parallel sides and measure the length of the segment connecting the two sides: it is the height of the parallelogram (h).
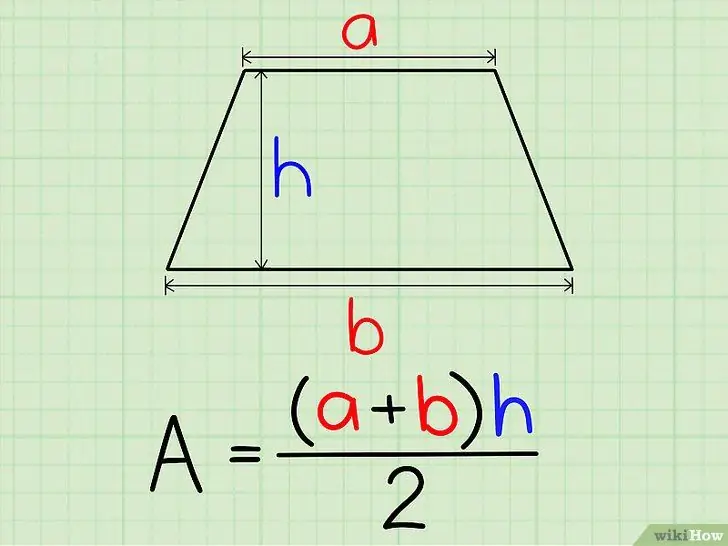
Step 3. Put these values into the formula A = 0, 5 (a + b) h
For more specific instructions, look for the article on how to calculate the area of a trapezoid
Method 5 of 10: Triangles
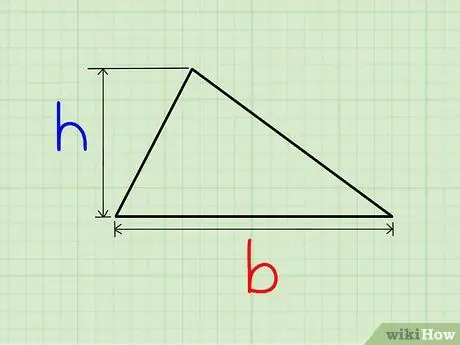
Step 1. Find the base and height of the triangle:
are the length of one side of the triangle (the base) and the length of the segment perpendicular to the base to the opposite vertex of the triangle.
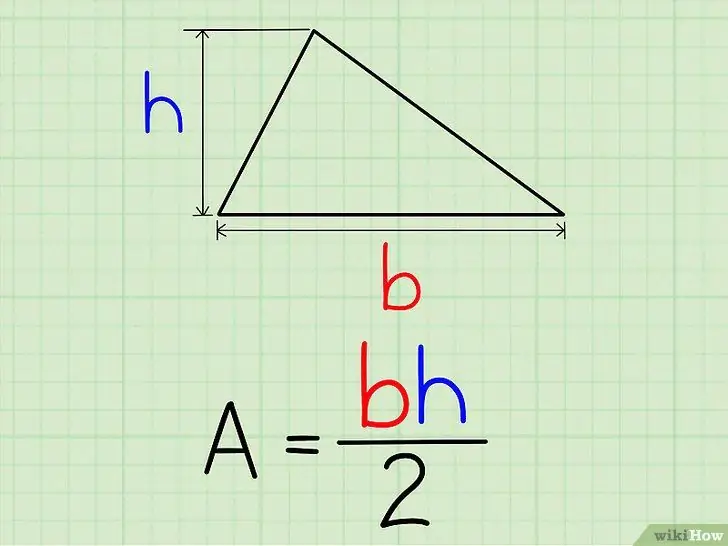
Step 2. To find the area, enter the base and height values into the expression A = 0.5 b * h
For more instructions, see the article on how to calculate the area of a triangle
Method 6 of 10: Regular Polygons
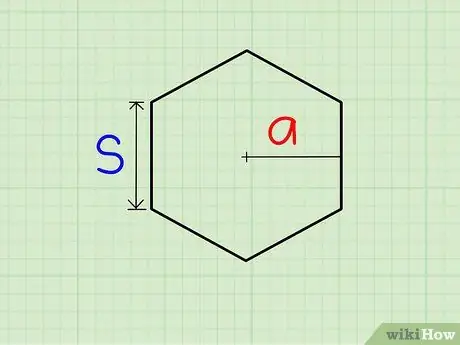
Step 1. Find the length of one side and the length of the apothem, which is the radius of the circle inscribed in the polygon
The variable a will be assigned to the length of the apothem.
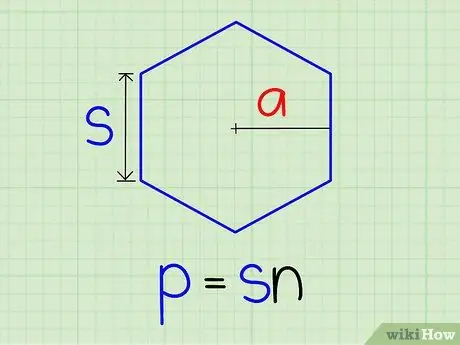
Step 2. Multiply the length of the single side by the number of sides to get the perimeter of the polygon (p)
Step 3. Insert these values into the expression A = 0, 5 a * p
For more specific instructions, read the article on how to find the area of regular polygons
Method 7 of 10: Circles
Step 1. Find the radius of the circle (r)
This is a line segment that connects the center to a point on the circumference. By definition, this value is constant no matter which point you choose on the circumference.
Step 2. Put the radius in the expression A = π r ^ 2
For more specific instructions, see the article on how to calculate the area of a circle
Method 8 of 10: Surface Area of a Prism

Step 1. Find the area of each side using the formula above for the area of a rectangle:
k = b * h
Step 2. Find the area of the bases using the above formulas to find the area of the appropriate polygon
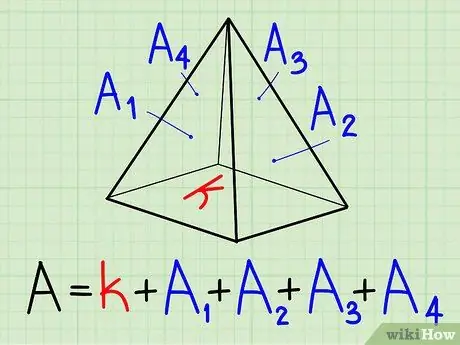
Step 3. Add all areas:
the two identical bases and all faces. Since the bases are the same, you can simply double the value of a base
For more extensive instructions, read the article on how to find the surface area of prisms
Method 9 of 10: Surface Area of a Cylinder

Step 1. Find the radius of one of the base circles
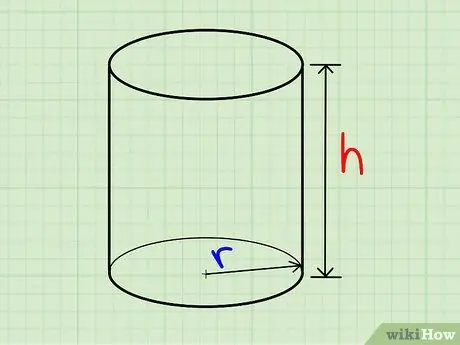
Step 2. Find the height of the cylinder

Step 3. Calculate the area of the bases using the formula for the area of a circle:
A = π r ^ 2
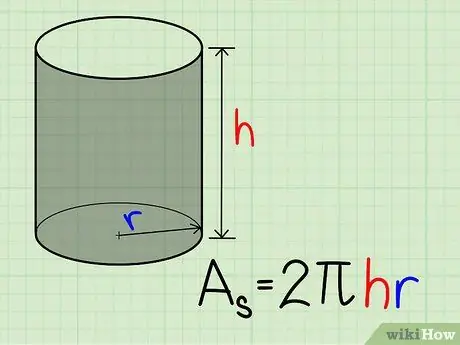
Step 4. Calculate the side area by multiplying the height of the cylinder by the perimeter of the base
The perimeter of a circle is P = 2πr, so the lateral area is A = 2πhr
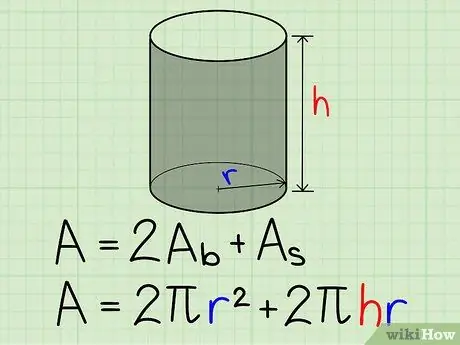
Step 5. Add all areas:
the two identical circular bases and the lateral surface. Thus, the total area should be S.t = 2πr ^ 2 + 2πhr.
For more in-depth instructions, take a look at the article on how to find the surface area of cylinders
Method 10 of 10: Area Underlying a Function
Suppose you need to find the area under a curve represented by the function f (x) and above the x axis in the domain interval [a, b]. This method requires knowledge of integral calculus. If you haven't taken an introductory calculus course, this method may not make any sense to you.
Step 1. Define f (x) in terms of x

Step 2. Compute the integral of f (x) in [a, b]
From the fundamental theorem of calculus, given F (x) = ∫f (x), to∫b f (x) = F (b) - F (a).
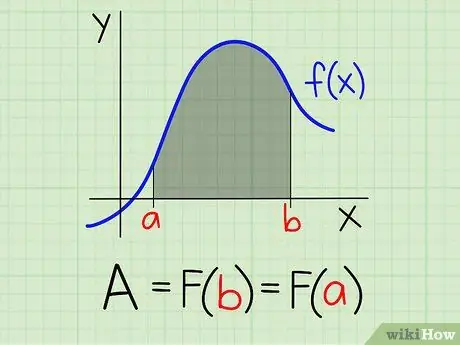
Step 3. Enter the values a and b into the integral expression
The area under the function f (x) for x between [a, b] is defined asto∫b f (x). Thus Area = F (b) - F (a).






