Linear equations with multiple unknowns are equations with two or more variables (usually represented by 'x' and 'y'). There are various ways to solve these equations, including elimination and substitution.
Steps
Method 1 of 3: Understanding the Components of Linear Equations
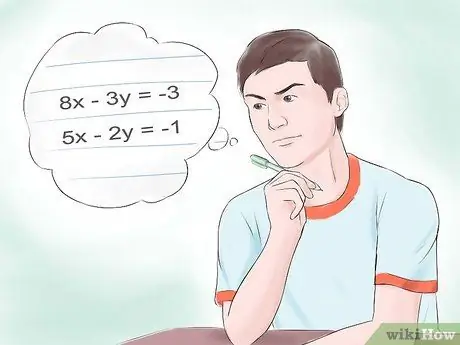
Step 1. What are multiple unknown equations?
Two or more linear equations grouped together are called a system. This means that a system of linear equations occurs when two or more linear equations are solved simultaneously. Eg:
- 8x - 3y = -3
- 5x - 2y = -1
- These are two linear equations that you have to solve at the same time, that is, you have to use both equations for solving.
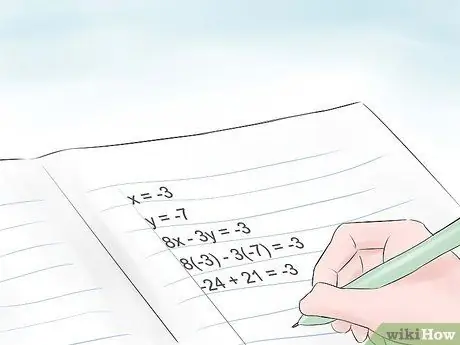
Step 2. You have to find the values of the variables, or unknowns
The solution of a problem with linear equations is a pair of numbers that makes both equations true.
In our example, you are trying to find the numerical values of 'x' and 'y' that make both equations true. In the example, x = -3 and y = -7. Put them in the equation. 8 (-3) - 3 (-7) = -3. IT IS TRUE. 5 (-3) -2 (-7) = -1. This is also TRUE
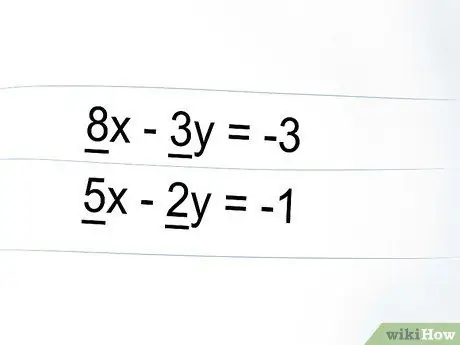
Step 3. What is a numerical coefficient?
The numerical coefficient is simply a number that precedes a variable. You will use numerical coefficients if you choose to use the elimination method. In our example, the numerical coefficients are:
8 and 3 in the first equation; 5 and 2 in the second equation

Step 4. Learn the difference between solving by deleting and solving by replacing
When you use the elimination method to solve a linear equation with multiple unknowns, you get rid of one of the variables you are working with (e.g. 'x') so that you can find the value of the other variable ('y'). When you find the value of 'y', you insert it into the equation to find that of 'x' (don't worry: we will see it in detail in Method 2).
Instead, you use the substitution method when you start solving a single equation so that you can find the value of one of the unknowns. After you solve it, you will insert the result into the other equation, effectively creating one longer equation instead of having two smaller ones. Again, don't worry - we'll cover it in detail in Method 3

Step 5. There can be linear equations with three or more unknowns
You can solve an equation with three unknowns in the same way you solve those with two unknowns. You can use both delete and replace; it will take a little more work to find the solutions, but the process is the same.
Method 2 of 3: Solve a Linear Equation with Elimination
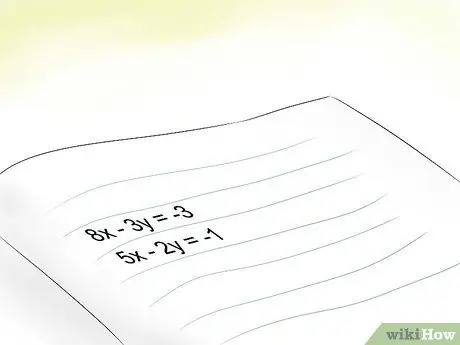
Step 1. Look at the equations
In order to solve them, you must learn to recognize the components of the equation. Let's use this example to learn how to eliminate unknowns:
- 8x - 3y = -3
- 5x - 2y = -1

Step 2. Choose a variable to delete
To eliminate a variable, its numerical coefficient (the number preceding the variable) must be opposite to the other equation (e.g. 5 and -5 are opposites). The aim is to get rid of one unknown, so as to be able to find the value of the other by eliminating one through subtraction. This means making sure that the coefficients of the same unknown in both equations cancel each other out. Eg:
- In 8x - 3y = -3 (equation A) and 5x - 2y = -1 (equation B), you can multiply equation A by 2 and equation B by 3, so that you get 6y in equation A and 6y in equation B.
- Equation A: 2 (8x - 3y = -3) = 16x -6y = -6.
- Equation B: 3 (5x - 2y = -1) = 15x -6y = -3

Step 3. Add or subtract the two equations to eliminate one of the unknowns and solve it to find the value of the other
Now that one of the unknowns can be eliminated, you can do so using addition or subtraction. Which one to use will depend on the one you need to eliminate the unknown. In our example, we will use subtraction, because we have 6y in both equations:
- (16x - 6y = -6) - (15x - 6y = -3) = 1x = -3. So x = -3.
- In other cases, if the numerical coefficient of x is not 1 after performing the addition or subtraction, we will need to divide both sides of the equation by the coefficient itself to simplify the equation.
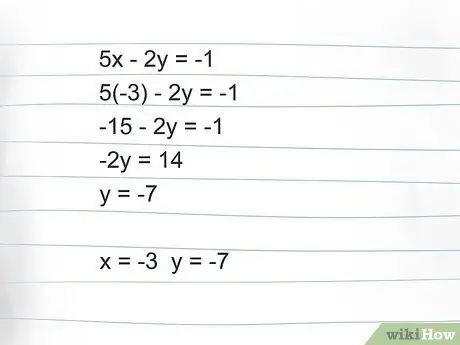
Step 4. Enter the obtained value to find the value of the other unknown
Now that you have found the value of 'x', you can insert it into the original equation to find the value of 'y'. When you see that it works in one of the equations, you can try to insert it in the other as well to check the correctness of the result:
- Equation B: 5 (-3) - 2y = -1 then -15 -2y = -1. Add 15 to both sides and you get -2y = 14. Divide both sides by -2 and you get y = -7.
- So x = -3 and y = -7.
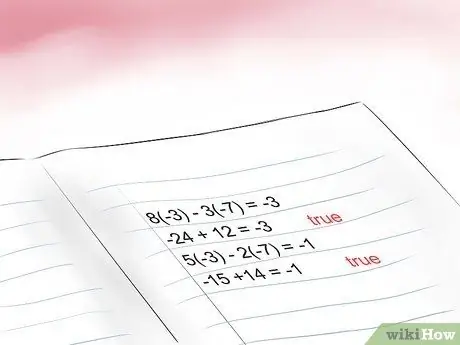
Step 5. Enter the values obtained in both equations to make sure they are correct
When you have found the values of the unknowns, enter them into the original equations to make sure they are correct. If any of the equations are not true with the values you found, you will have to try again.
- 8 (-3) - 3 (-7) = -3 so -24 +21 = -3 TRUE.
- 5 (-3) -2 (-7) = -1 so -15 + 14 = -1 TRUE.
- So, the values you got are correct.
Method 3 of 3: Solve a Linear Equation with Substitution
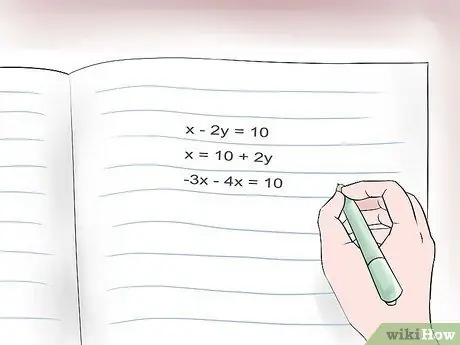
Step 1. Start by solving one of the equations for one of the variables
It doesn't matter which equation you decide to start with, nor which variable you choose to find first: either way, you'll get the same solutions. However, it's best to make the process as simple as possible. You should start with the equation that seems simpler to you to solve. So, if there is an equation with a coefficient of value 1, such as x - 3y = 7, you could start from this one, because it will be easier to find 'x'. For example, our equations are:
- x - 2y = 10 (equation A) and -3x -4y = 10 (equation B). You could start solving x - 2y = 10 since the coefficient of x in this equation is 1.
- Solving equation A for x would mean adding 2y to both sides. So x = 10 + 2y.
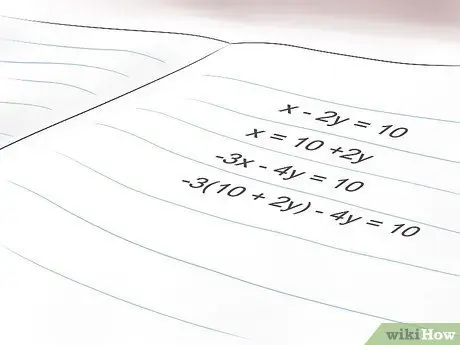
Step 2. Substitute what you got in Step 1 into the other equation
In this step, you must enter (or replace) the solution found for 'x' in the equation that you have not used. This will allow you to find the other unknown, in this case 'y'. Give it a go:
Insert the 'x' of equation B into equation A: -3 (10 + 2y) -4y = 10. As you can see, we have eliminated 'x' from the equation and inserted what 'x' is equal to
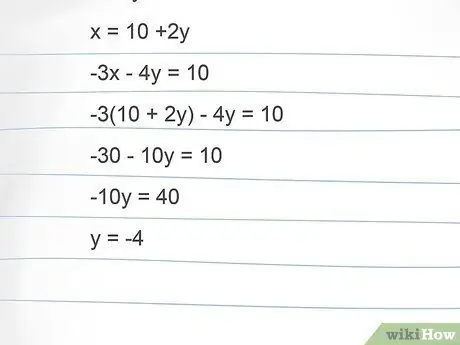
Step 3. Find the value of the other unknown
Now that you have eliminated one of the unknowns from the equation, you can find the value of the other. It is simply a matter of solving a normal linear equation with one unknown. Let's solve the one in our example:
- -3 (10 + 2y) -4y = 10 so -30 -6y -4y = 10.
- Add the y's: -30 - 10y = 10.
- Move -30 to the other side (changing the sign): -10y = 40.
- Solve to find y: y = -4.
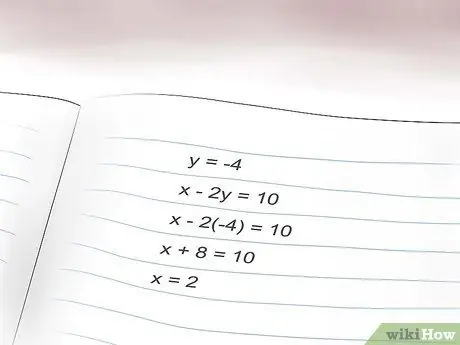
Step 4. Find the second unknown
To do this, enter the value of 'y' (or the first unknown) that you found in one of the original equations. Then solve it to find the value of the other unknown, in this case 'x'. Let's try:
- Find 'x' in equation A by inserting y = -4: x - 2 (-4) = 10.
- Simplify the equation: x + 8 = 10.
- Solve to find x: x = 2.
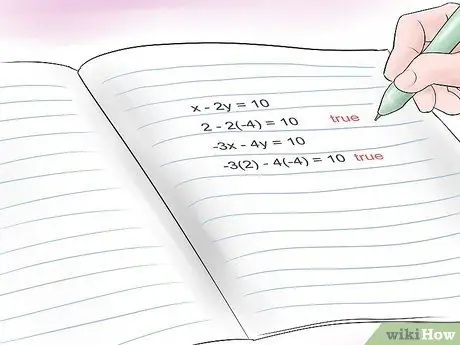
Step 5. Check that the values you found work in all equations
Insert both values into each equation to make sure you get true equations. Let's see if our values work:
- The equation A: 2 - 2 (-4) = 10 is TRUE.
- Equation B: -3 (2) -4 (-4) = 10 is TRUE.
Advice
- Pay attention to the signs; Since many basic operations are used, changing signs can change each step of the calculations.
- Check the final results. You can do this by substituting the obtained values to the corresponding variables in all the original equations; if the results of both sides of the equation coincide, the results you have found are correct.






