First degree algebraic equations are relatively simple and quick to solve: most of the time two steps are enough to arrive at the final result. The procedure consists in isolating the unknown to the right or left of the equality sign using the addition, subtraction, multiplication or division operations. If you want to learn how to solve first degree equations in many different ways, read on!
Steps
Method 1 of 3: Equations with an Unknown

Step 1. Write down the problem
The first thing to do in solving an equation is to write it down, so you can start visualizing the solution. Suppose we need to work with this problem: -4x + 7 = 15.
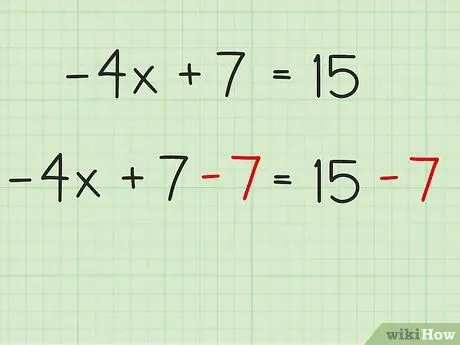
Step 2. Decide whether to use addition or subtraction to isolate the unknown
The next step is to leave the term "-4x" on one side of the equation and put all the other constants (integers) on the other. To do this you have to "add the inverses", that is, find the inverse of +7, which is -7. Subtract 7 from both sides of the equation so that "+7", which is on the same side of the variable, eliminates itself. Then write "-7" below 7 and below 15, so that the equation stays balanced.
Remember the golden rule of algebra
Whatever arithmetic manipulation you do on one side of the equation you must also do it on the other, in order to keep the sign of equality valid; that's why you have to subtract 7 from 15. You have to subtract the value 7 once per side; for this reason the operation must not be repeated again.

Step 3. Add or subtract the constant on both sides of the equation
This completes the variable isolation process. When you subtract 7 from +7 on the left side, you delete the constant. When you subtract 7 from +15 to the right of the equality sign, you get 8. For this reason you can rewrite the equation as follows: -4x = 8.
- -4x + 7 = 15 =
- -4x = 8.

Step 4. Eliminate the coefficient of the unknown with a multiplication or division
The coefficient is the number written to the left of the variable and by which it is multiplied. In our example -4 is the coefficient of x. To remove -4 from -4x you need to divide both sides of the equation by -4. This is because the unknown is multiplied by -4 and the opposite of multiplication is the division that must be performed on both sides of the equality.
Remember that when you perform an operation on one side of the equality sign, you must also do it on the other. That's why you will see the "÷ -4" twice.

Step 5. Solve for the unknown
To proceed, divide the left side of the equation (-4x) by -4 and you get x. Divide the right side of equation (8) by -4 and you get -2. Hence: x = -2. It took two steps (one subtraction and one division) to solve this equation.
Method 2 of 3: Equations with an Unknown in Each Side

Step 1. Write down the problem
Suppose the equation in question is: -2x - 3 = 4x - 15. Before continuing, check that the variables are equal. In this case "-2x" and "4x" have the same unknown "x", so you can continue with the calculations.
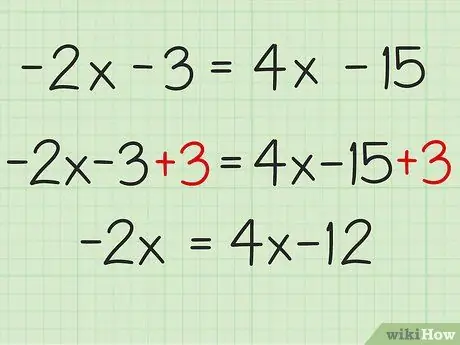
Step 2. Move the constants to the right side of the equality sign
To do this, you will have to use addition or subtraction, so as to eliminate the constants that are on the left side. The constant is -3, so you have to take its opposite (+3) and add it up on both sides.
- Adding +3 to the left side you get: (-2x-3) +3 = -2x.
- Adding +3 to the right side you get: (4x-15) +3 = 4x-12.
- So: (-2x - 3) +3 = (4x - 15) +3 = -2x = 4x - 12.
- The new equation is -2x = 4x -12.
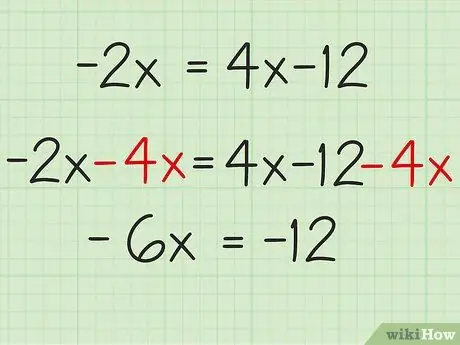
Step 3. Move the variables to the left side of the equation
To do this, you need to find the "opposite" of "4x", which is "-4x", and subtract it on both sides. On the left you will get: -2x - 4x = -6x; on the right you get: (4x -12) -4x = -12. The new equation can be rewritten as -6x = -12
2x - 4x = (4x - 12) - 4x = -6x = -12
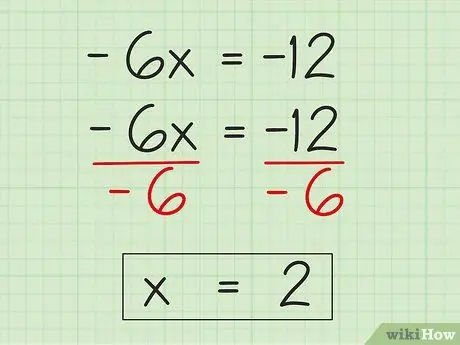
Step 4. Solve for the variable
Now that you have simplified the equation to the form -6x = -12, all you have to do is divide both sides by -6 to isolate the unknown x, which is multiplied by the coefficient -6. On the left you will get: -6x ÷ -6 = x. On the right you get: -12 ÷ -6 = 2. So: x = 2.
- -6x ÷ -6 = -12 ÷ -6.
- x = 2.
Method 3 of 3: Other Methods

Step 1. Solve the first degree equations leaving the unknown to the right of the equality sign
Equations can also be solved by leaving the variable term to the right. Once it has been isolated, the result does not change. Let us consider the problem 11 = 3 - 7x. First, it “shifts” the constants by subtracting 3 on both sides of the equation. Then divide them by -7 and solve for x. Here's how to proceed:
- 11 = 3 - 7x =
- 11 - 3 = 3 - 3 - 7x =
- 8 = - 7x =
- 8 / -7 = -7 / 7x
- -8/7 = x i.e. -1.14 = x

Step 2. Solve the first degree equation by multiplying instead of dividing
The basic principle for solving this kind of problem is always the same: use arithmetic to combine constants, isolate the variable term without coefficient. Let us consider the equation x / 5 + 7 = -3. The first thing to do is subtract 7 from both sides; then you can multiply them by 5 and solve for x. Here are the step-by-step calculations:
- x / 5 + 7 = -3 =
- (x / 5 + 7) - 7 = -3 - 7 =
- x / 5 = -10
- x / 5 * 5 = -10 * 5
- x = -50.
Advice
- When you divide or multiply two numbers with opposite signs (i.e. one negative and one positive) the result is always negative. If the signs are the same, the solution is a positive number.
- If there is no number to the left of the x, it is treated as 1x.
- There may not be an explicit constant on each side of the equation. If there is no number after x, it is treated as x + 0.






