In a "system of equations" you are required to solve two or more equations at the same time. When there are two different variables, such as x and y or a and b, it might seem like a difficult task, but only at first glance. Fortunately, once you have learned the method to apply, all you will need is some basic knowledge of algebra. If you prefer to learn visually, or your teacher also requires a graphical representation of the equations, then you must also learn how to create a graph. Graphs are useful for "seeing how equations behave" and for verifying work, but it is a slower method that doesn't lend itself very well to systems of equations.
Steps
Method 1 of 3: By Replacement

Step 1. Move the variables to the sides of the equations
To begin this "substitution" method, you must first "solve for x" (or any other variable) one of the two equations. For example, in the equation: 4x + 2y = 8, rewrite the terms by subtracting 2y from each side to get: 4x = 8 - 2y.
Later, this method involves the use of fractions. If you don't like working with fractions, try the elimination method which will be explained later

Step 2. Divide both sides of the equation to "solve it for x"
Once you've moved the variable x (or the one you've chosen) to one side of the equality sign, divide both terms to isolate it. Eg:
- 4x = 8 - 2y.
- (4x) / 4 = (8/4) - (2y / 4).
- x = 2 - ½y.
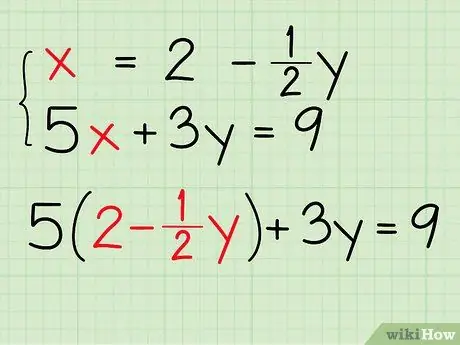
Step 3. Enter this value in the other equation
Be sure to consider the second equation now and not the one you have already worked on. Within this equation, replace the value of the variable you found. Here's how to proceed:
- You know that x = 2 - ½y.
- The second equation, which you haven't worked out yet is: 5x + 3y = 9.
- In this second equation replace the variable x with "2 - ½y" and you get 5 (2 - ½y) + 3y = 9.

Step 4. Solve the equation that has only one variable
Use classic algebraic techniques to find its value. If this process deletes the variable, go to the next step.
Otherwise find the solution for one of the equations:
- 5 (2 - ½y) + 3y = 9.
- 10 - (5/2) y + 3y = 9.
- 10 - (5/2) y + (6/2) y = 9 (If you haven't understood this step, read how to add fractions together. This is a calculation that occurs often, though not always, in this method).
- 10 + ½y = 9.
- ½y = -1.
- y = -2.
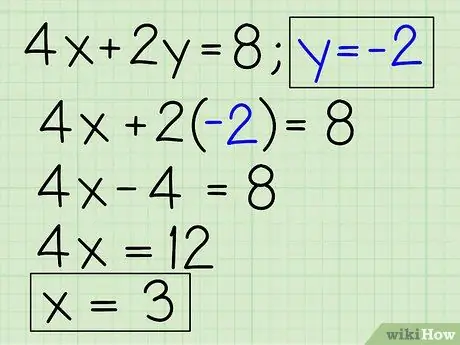
Step 5. Use the solution you found to find the value of the first variable
Don't make the mistake of leaving the problem half unsolved. Now you have to enter the value of the second variable within the first equation, so as to find the solution for x:
- You know that y = -2.
- One of the original equations is 4x + 2y = 8 (You can use any of the equations for this step).
- Insert -2 in place of y: 4x + 2 (-2) = 8.
- 4x - 4 = 8.
- 4x = 12.
- x = 3.

Step 6. Now let's see what to do in case both variables cancel each other out
When you enter x = 3y + 2 or a similar value in another equation, you are trying to reduce an equation with two variables to an equation with one variable. However, sometimes, it happens that the variables cancel each other out and you get an equation without variables. Double-check your calculations to make sure you haven't made any mistakes. If you are sure you have done everything correctly, you should get one of the following results:
- If you get a variable-free equation that is not true (e.g. 3 = 5) then the system has no solution. If you graph the equations you will find that these are two parallel lines that will never intersect.
- If you get a variable-free equation that is true (like 3 = 3) then the system has infinite solutions. Its equations are exactly identical to each other and if you draw the graphical representation you get the same line.
Method 2 of 3: A Elimination
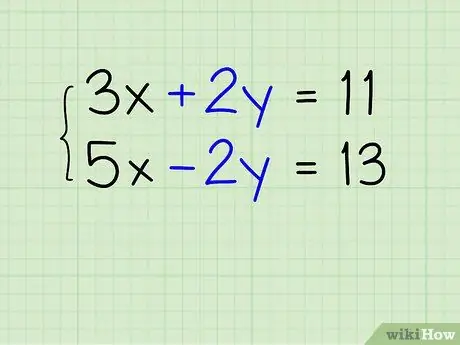
Step 1. Find the variable to delete
Sometimes, equations are written in such a way that a variable can "already be eliminated". For example when the system is composed of: 3x + 2y = 11 And 5x - 2y = 13. In this case "+ 2y" and "-2y" cancel each other out and the variable "y" can be removed from the system. Analyze the equations and find one of the variables that can be cleared. If you find that this is not possible, go to the next step.

Step 2. Multiply an equation to delete a variable
Skip this step if you have already deleted a variable. If there are no naturally eliminable variables, you have to manipulate the equations. This process is best explained with an example:
- Suppose you have a system of equations: 3x - y = 3 And - x + 2y = 4.
- Let's change the first equation so that we can cancel the y. You could also do this with the x always getting the same result.
- The variable - y of the first equation must be eliminated with + 2y of the second. To make this happen, multiply - y for 2.
- Multiply both terms of the first equation by 2 and you get: 2 (3x - y) = 2 (3) so 6x - 2y = 6. Now you can delete - 2y with + 2y of the second equation.
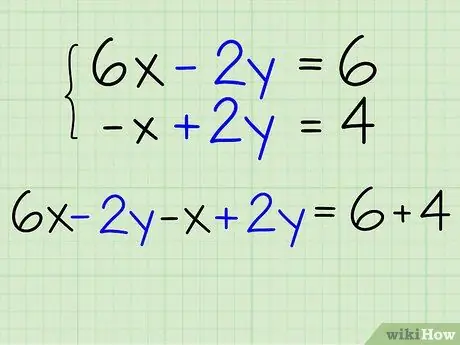
Step 3. Combine the two equations
To do this, add the terms on the right of both equations together and do the same for the terms on the left. If you've edited the equations correctly, the variables should clear. Here is an example:
- Your equations are 6x - 2y = 6 And - x + 2y = 4.
- Add the left sides together: 6x - 2y - x + 2y =?
- Add the sides on the right together: 6x - 2y - x + 2y = 6 + 4.
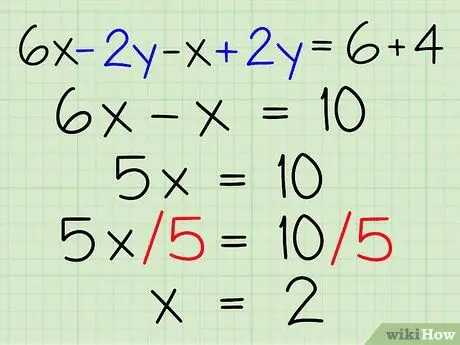
Step 4. Solve the equation for the remaining variable
Simplify the combined equation using basic algebra techniques. If there are no variables after simplification, go to the last step of this section. Otherwise complete the calculations to find the value of a variable:
- You have the equation 6x - 2y - x + 2y = 6 + 4.
- Group the unknowns x And y: 6x - x - 2y + 2y = 6 + 4.
- Simplify: 5x = 10.
- Solve for x: (5x) / 5 = 10/5 so x = 2.
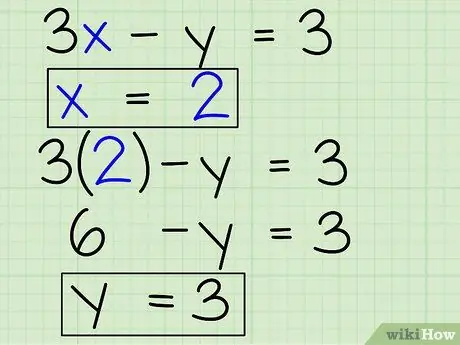
Step 5. Find the value of the other unknown
Now you know one of the two variables but not the second. Enter the value you found in one of the original equations and do the calculations:
- Now you know that x = 2 and one of the original equations is 3x - y = 3.
- Replace the x with 2: 3 (2) - y = 3.
- Solve for y: 6 - y = 3.
- 6 - y + y = 3 + y therefore 6 = 3 + y.
- 3 = y.
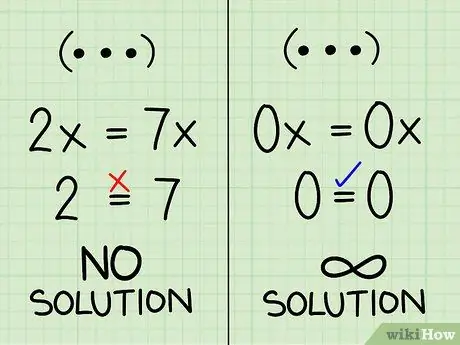
Step 6. Let us consider the case that both unknowns cancel each other out
Sometimes, by combining the equations of a system, the variables disappear, making the equation meaningless and useless for your purposes. Always check your calculations to make sure you haven't made any mistakes and write one of these answers as your solution:
- If you have combined the equations and you have obtained one with no unknowns and which is not true (like 2 = 7) then the system has no solution. If you draw a graph you will get two parallels that never cross.
- If you have combined the equations and got one with no unknowns and true (like 0 = 0) then they are there infinite solutions. The two equations are perfectly identical and if you draw the graphical representation you get the same line.
Method 3 of 3: With the Chart

Step 1. Use this method only if prompted
Unless you are using a computer or graphing calculator, you will be able to solve most systems only by approximation. Your teacher or textbook will ask you to apply the graphing method just for you to practice representing equations. However, you can also use it to verify your work after finding the solutions with the other procedures.
The basic concept is to plot both equations on a graph and find the points where the plots cross (the solutions). The values of x and y represent the coordinates of the system
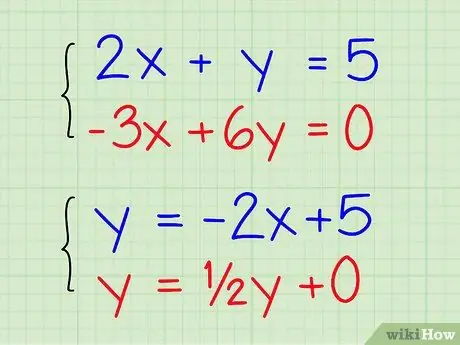
Step 2. Solve both equations for y
Keep them separate but rewrite them by isolating the y to the left of the equality sign (use simple algebraic steps). Eventually you should get the equations in the form of "y = _x + _". Here is an example:
- Your first equation is 2x + y = 5, change it to y = -2x + 5.
- Your second equation is - 3x + 6y = 0, change it to 6y = 3x + 0 and simplify it as y = ½x + 0.
- If you get two identical equations the same line will be a single "intersection" and you can write that there are infinite solutions.
Step 3. Draw the Cartesian axes
Take a sheet of graph paper and draw the vertical "y" axis (called the ordinates) and the horizontal "x" axis (called the abscissa). Starting from the point where they intersect (origin or point 0; 0) write the numbers 1, 2, 3, 4 and so on on the vertical (upward) and horizontal (right) axis. Write the numbers -1, -2 on the y axis from the origin downwards and on the x axis from the origin to the left.
- If you don't have graph paper, use a ruler and be precise in spacing the numbers evenly.
- If you need to use large numbers or decimals, you can change the scale of the graph (e.g. 10, 20, 30 or 0, 1; 0, 2 and so on).
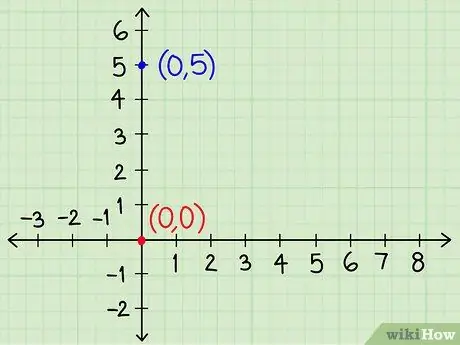
Step 4. Plot the intercept for each equation
Now that you have transcribed these as y = _x + _, you can start drawing a point corresponding to the intercept. This means setting y equal to the last number of the equation.
-
In our previous examples, an equation (y = -2x + 5) intersects the y axis at the point
Step 5., the other one (y = ½x + 0) at the point 0. These correspond to the coordinate points (0; 5) and (0; 0) on our graph.
- Use different colored pens to draw the two lines.
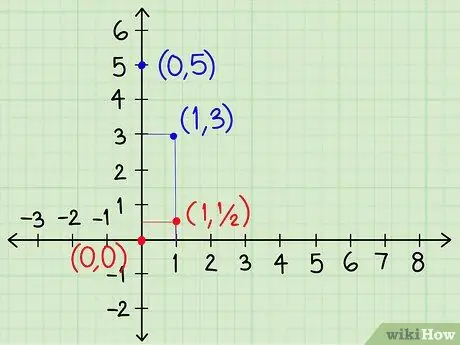
Step 5. Use the angular coefficient to continue drawing the lines
in the form y = _x + _, the number in front of the unknown x is the angular coefficient of the line. Each time the value of x increases by one unit, the value of y increases by as many times as the angular coefficient. Use this information to find the point of each line for the value of x = 1. Alternatively, set x = 1 and solve the equations for y.
- We keep the equations of the previous example and we obtain that y = -2x + 5 has an angular coefficient of - 2. When x = 1, the line moves downwards by 2 positions with respect to the point occupied for x = 0. Draw the segment connecting the point with coordinates (0; 5) and (1; 3).
- The equation y = ½x + 0 has an angular coefficient of ½. When x = 1 the line rises by ½ space with respect to the point corresponding to x = 0. Draw the segment joining the coordinate points (0; 0) and (1; ½).
- If the lines have the same angular coefficient they are parallel to each other and will never intersect. The system has no solution.
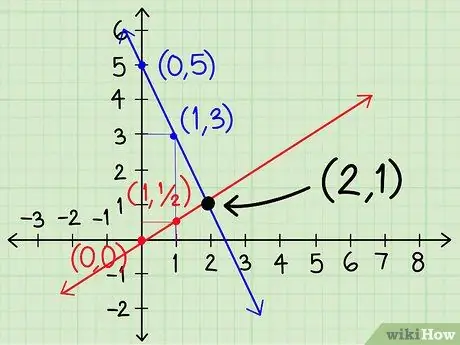
Step 6. Keep finding the various points for each equation until you find that the lines intersect
Stop and look at the graph. If the lines have already crossed, follow the next step. Otherwise make a decision based on how the lines behave:
- If the lines converge on each other, it continues to find points in that direction.
- If the lines move away from each other, then go back and starting from the points with abscissa x = 1 proceed in the other direction.
- If the lines do not seem to approach in any direction, then stop and try again with points more distant from each other, for example with abscissa x = 10.
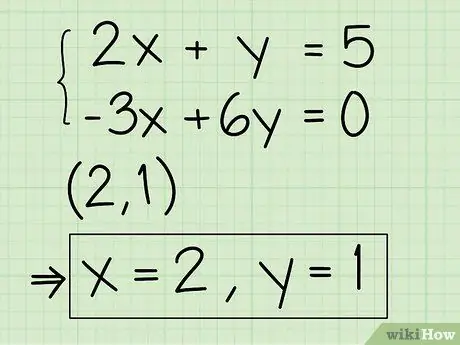
Step 7. Find the solution to the intersection
When the lines cross, the x and y coordinate values represent the answer to your problem. If you are lucky, they will also be whole numbers. In our example, the lines of intersect a (2;1) then you can write the solution as x = 2 and y = 1. In some systems, the lines will intersect at points between two integers, and unless your graph is extremely accurate, it will be difficult to determine the value of the solution. If this happens, you can formulate your answer as "1 <x <2" or use the substitution or deletion method to find a precise solution.
Advice
- You can check your work by inserting the solutions you got into the original equations. If you get a true equation (for example 3 = 3), then your solution is correct.
- In the elimination method, sometimes you will have to multiply an equation by a negative number in order to delete a variable.






