6 Ways to Factor Second Degree Polynomials (Quadratic Equations)

2024 Author: Samantha Chapman | [email protected]. Last modified: 2023-12-17 09:13

A polynomial contains a variable (x) raised to a power, called "degree", and several terms and / or constants. Decomposing a polynomial means reducing the expression to smaller ones that are multiplied together. It is a skill that is learned in algebra courses and can be difficult to understand if you are not at this level.

Steps

To begin

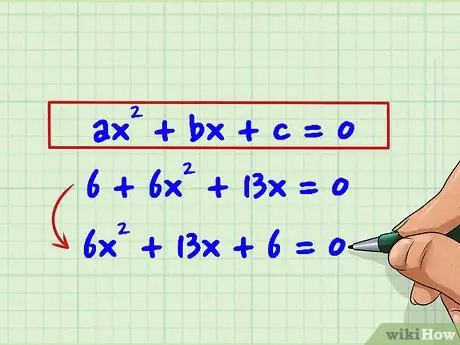
Step 1. Order your expression

The standard format for the quadratic equation is: ax² + bx + c = 0 Start by sorting the terms of your equation from highest to lowest degree, just like in the standard format. For example, let's take: 6 + 6x² + 13x = 0 Let's reorder this expression by simply moving the terms so that it is easier to solve: 6x² + 13x + 6 = 0

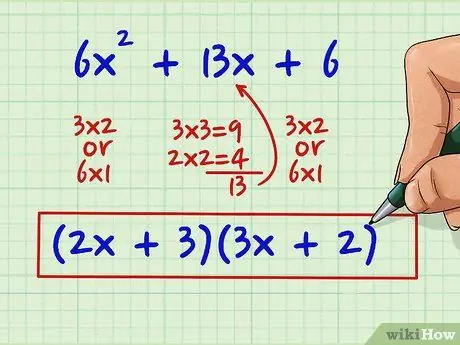
Step 2. Find the factored form using one of the methods listed below

The factoring or factoring of the polynomial will result in two smaller expressions which can be multiplied to return to the original polynomial: 6 x² + 13 x + 6 = (2 x + 3) (3 x + 2) In this example, (2 x + 3) and (3 x + 2) are factors of the original expression, 6x² + 13 x + 6.

Step 3. Check your work

Multiply the factors identified. After that, combine the similar terms and you are done. It starts with: (2 x + 3) (3 x + 2) Let's try to multiply each term of the first expression with each term of the second, obtaining: 6x² + 4x + 9x + 6 From here, we can add 4 x and 9 x as they are all similar terms. We know that our factors are correct because we get the starting equation: 6x² + 13x + 6

Method 1 of 6: Proceed by Attempts

If you have a fairly simple polynomial, you may be able to understand its factors just by looking at it. For example, with practice, many mathematicians are able to know that the expression 4 x² + 4 x + 1 has as factors (2 x + 1) and (2 x + 1) right after seeing so many times. (This obviously won't be easy with the more complicated polynomials.) In this example we use a less common expression:

3 x² + 2x - 8

Step 1. We list the factors of term 'a' and term 'c'

Using the ax expression format ² + bx + c = 0, identify the terms 'a' and 'c' and list which factors they have. For 3x² + 2x - 8, it means: a = 3 and has a set of factors: 1 * 3 c = -8 and has four sets of factors: 4 * -2, -4 * 2, -8 * 1 and -1 * 8.

Step 2. Write two sets of brackets with blanks

You will be able to insert the constants within the space you left in each expression: (x) (x)

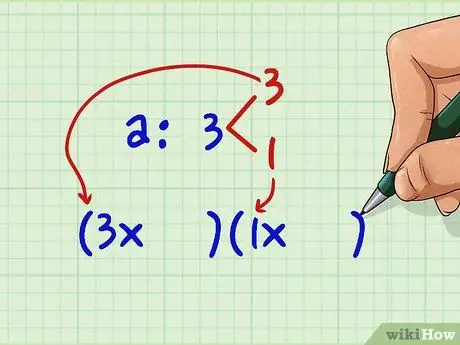
Step 3. Fill in the spaces in front of the x with a couple of possible factors of the 'a' value

For the term 'a' in our example, 3 x², there is only one possibility: (3x) (1x)

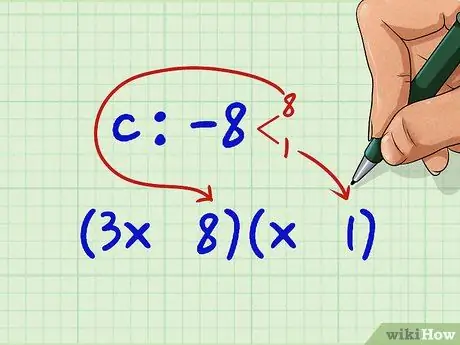
Step 4. Fill in two spaces after the x with a couple of factors for the constants

Suppose you have chosen 8 and 1. Write them: (3x

Step 8.)(

Step 1

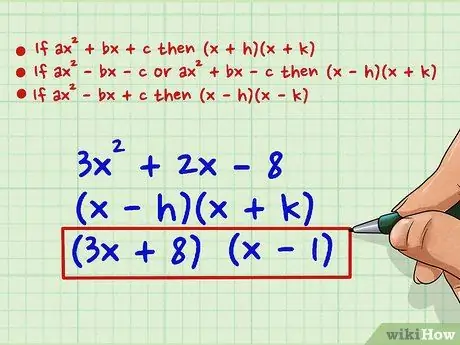
Step 5. Decide what signs (plus or minus) there should be between the variables x and the numbers

According to the signs of the original expression, it is possible to understand what the signs of the constants should be. We will call 'h' and 'k' the two constants for our two factors: If ax² + bx + c then (x + h) (x + k) If ax² - bx - c or ax² + bx - c then (x - h) (x + k) If ax² - bx + c then (x - h) (x - k) For our example, 3x² + 2x - 8, the signs must be: (x - h) (x + k), with two factors: (3x + 8) and (x - 1)

Step 6. Test your choice using multiplication between terms

A quick test to run is to see if at least the mean term is of the correct value. If not, you may have chosen the wrong 'c' factors. Let's check our answer: (3 x + 8) (x-1) Multiplying, we arrive at: 3 x ² - 3 x + 8x - 8 By simplifying this expression by adding terms like (-3x) and (8x), we get: 3 x² - 3 x + 8x - 8 = 3 x² + 5 x - 8 We now know that we must have identified the wrong factors: 3x² + 5x - 8 ≠ 3x² + 2x - 8

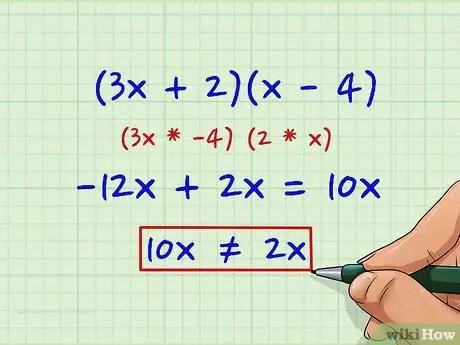
Step 7. Reverse your choices if necessary

In our example, we try 2 and 4 instead of 1 and 8: (3 x + 2) (x-4) Now our term c is a -8, but our outer / inner product (3x * -4) and (2 * x) is -12x and 2x, which do not combine to make the term correct b + 2x.-12x + 2x = 10x 10x ≠ 2x

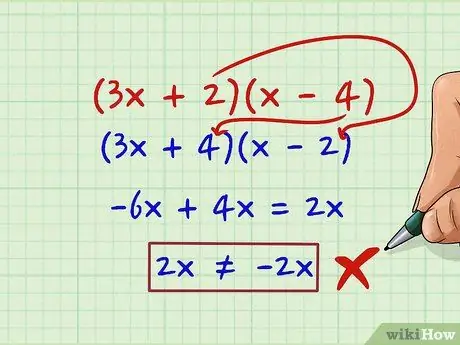
Step 8. Reverse the order, if necessary

Let's try to move the 2 and 4: (3x + 4) (x - 2) Now our term c (4 * 2 = 8) is still fine, but the outer / inner products are -6x and 4x. If we combine them: -6x + 4x = 2x 2x ≠ -2x We are close enough to the 2x we were aiming for, but the sign is wrong.

Step 9. Recheck the marks if necessary

We go in the same order, but reverse the one with the minus: (3x- 4) (x + 2) Now the term c is still okay and the external / internal products are now (6x) and (-4x). Since: 6x - 4x = 2x 2x = 2x We can now recognize from the original text that 2x is positive. They have to be the correct factors.

Method 2 of 6: Break it down

This method identifies all possible factors of the terms 'a' and 'c' and uses them to figure out what the factors should be. If the numbers are very large or if the other guesswork seems to take too long, use this method. Let's use the example:

6x² + 13x + 6

Step 1. Multiply term a with term c

In this example, a is 6 and c is again 6.6 * 6 = 36

Step 2. Find the term 'b' by decomposing and trying

We are looking for two numbers that are factors of the product 'a' * 'c' that we have identified and add the term 'b' (13). 4 * 9 = 36 4 + 9 = 13

Step 3. Substitute the two numbers obtained in the equation as the sum of the term 'b'

We use 'k' and 'h' to represent the two numbers we got, 4 and 9: ax² + kx + hx + c 6x² + 4x + 9x + 6

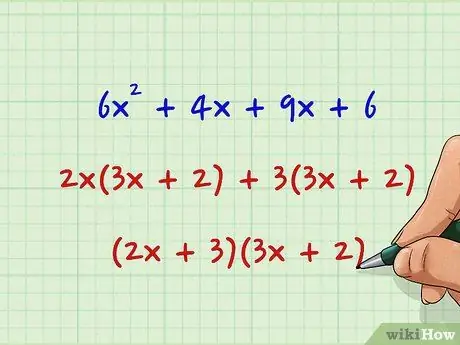
Step 4. We factor the polynomial with the grouping

Organize the equation so that you can bring out the largest common factor between the first two terms and the last two. Both of the remaining factored groups should be the same. Put together the greatest common divisors and enclose them in parentheses next to the factored group; the result will be given by your two factors: 6x² + 4x + 9x + 6 2x (3x + 2) + 3 (3x + 2) (2x + 3) (3x + 2)

Method 3 of 6: Triple Play

Similar to the decomposition method, the 'triple play' method examines the possible factors of the product 'a' by 'c' and uses them to figure out what 'b' should be. Consider this example equation:

8x² + 10x + 2

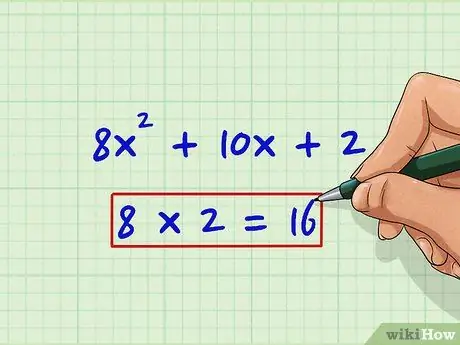
Step 1. Multiply the term 'a' with the term 'c'

As with the decomposition method, this will help us identify possible candidates for the 'b' term. In this example, 'a' is 8 and 'c' is 2.8 * 2 = 16

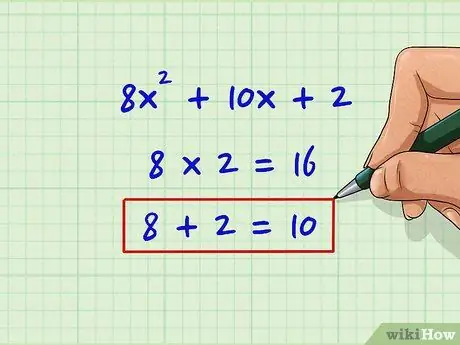
Step 2. Find two numbers that have this value as a product and the term 'b' as a sum

This step is identical to the decomposition method - we are testing and excluding the possible values of the constants. The product of the terms 'a' and 'c' is 16 and the sum is 10: 2 * 8 = 16 8 + 2 = 10

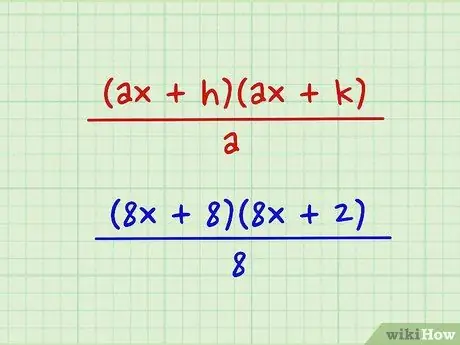
Step 3. Take these two numbers and try to substitute them in the 'triple play' formula

Take our two numbers from the previous step - let's call them 'h' and 'k' - and put them in this expression: ((ax + h) (ax + k)) / a At this point we would get: ((8x + 8) (8x + 2)) / 8

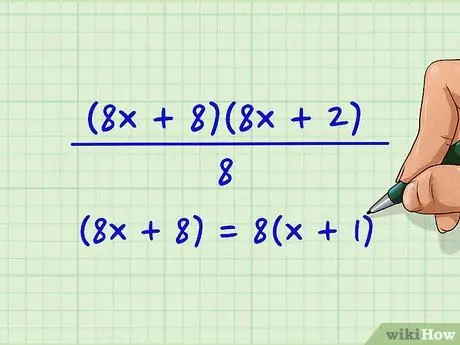
Step 4. See if one of the two terms in the numerator is divisible by 'a'

In this example, we are checking whether (8 x + 8) or (8 x + 2) can be divided by 8. (8 x + 8) is divisible by 8, so we divide this term by 'a' and leave the other as it is. (8 x + 8) = 8 (x + 1) The found term is what's left after dividing the term by 'a': (x + 1)

Step 5. Extract the greatest common divisor from one or both terms, if any

In this example, the second term has a GCD of 2, because 8 x + 2 = 2 (4x + 1). Combine this answer with the term identified in the previous step. These are the factors of your equation. 2 (x + 1) (4x + 1)

Method 4 of 6: Difference of Two Squares

Some coefficients of polynomials can be identified as 'squares' or products of two numbers. Identifying these squares allows you to make the decomposition of some polynomials much faster. Consider the equation:

27x² - 12 = 0

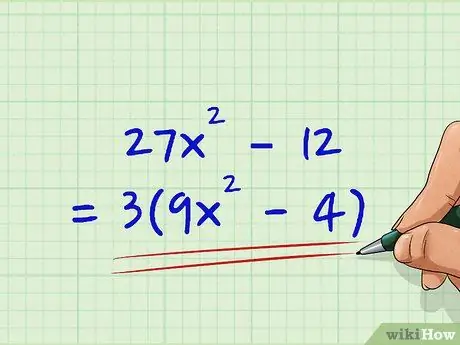
Step 1. Extract the greatest common divisor, if possible

In this case, we can see that 27 and 12 are both divisible by 3, so we get: 27x² - 12 = 3 (9x² - 4)

Step 2. Try to check if the coefficients of your equation are squares

To use this method you should be able to take the square root of the perfect squares. (Note that we omit negative signs - since these numbers are squares, they can be products of two negative or two positive numbers) 9x² = 3x * 3x and 4 = 2 * 2

Step 3. Using the square roots found, write down the factors

We take the values 'a' and 'c' from our previous step, 'a' = 9 and 'c' = 4, after which we find their square roots, √ 'a' = 3 and √ 'c' = 2. These are the coefficients of the simplified expressions: 27x² - 12 = 3 (9x² - 4) = 3 (3x + 2) (3x - 2)

Method 5 of 6: Quadratic Formula

If all else fails and the equation cannot be factored, use the quadratic formula. Consider the example:

x² + 4x + 1 = 0

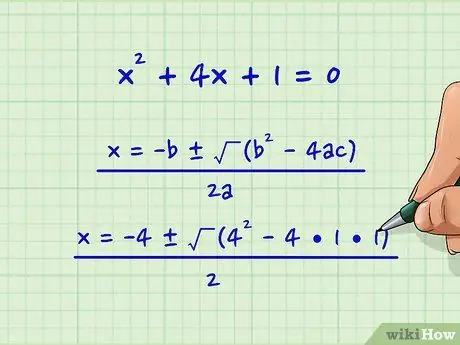
Step 1. Enter the corresponding values into the quadratic formula:

x = -b ± √ (b² - 4ac) --------------------- 2a We get the expression: x = -4 ± √ (4² - 4•1•1) / 2

Step 2. Solve the x

You should get two x values. As shown above, we get two answers: x = -2 + √ (3) and also x = -2 - √ (3)

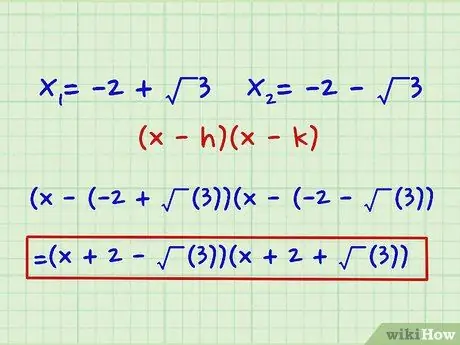
Step 3. Use the value of x to find the factors

Insert the obtained x values as they were constants in the two polynomial expressions. These will be your factors. If we call our two answers 'h' and 'k', we write the two factors like this: (x - h) (x - k) In this case, our definitive answer is: (x - (-2 + √ (3)) (x - (-2 - √ (3)) = (x + 2 - √ (3)) (x + 2 + √ (3))

Method 6 of 6: Using a Calculator

If you are licensed to use a graphing calculator, it makes the decomposition process much easier, especially on standardized tests. These instructions are for a Texas Instruments graphing calculator. Let's use the example equation:

y = x² - x - 2

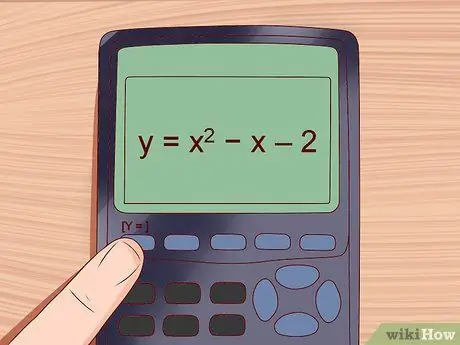
Step 1. Enter the equation in the screen [Y =]

Step 2. Draw the trend of the equation using the calculator

Once you have entered your equation, press [GRAPH]: you should see a continuous arc representing the equation (and it will be an arc since we are dealing with polynomials).

Step 3. Find where the arc intersects the x axis

Since polynomial equations are traditionally written as ax² + bx + c = 0, these are the two values of x that make the expression equal to zero: (-1, 0), (2, 0) x = -1, x = 2

If you cannot locate the points manually, press [2nd] and then [TRACE]. Press [2] or select zero. Move the cursor to the left of an intersection and press [ENTER]. Move the cursor to the right of an intersection and press [ENTER]. Scroll the cursor as close as possible to an intersection and press [ENTER]. The calculator will find the value of x. Repeat the same thing for the second intersection

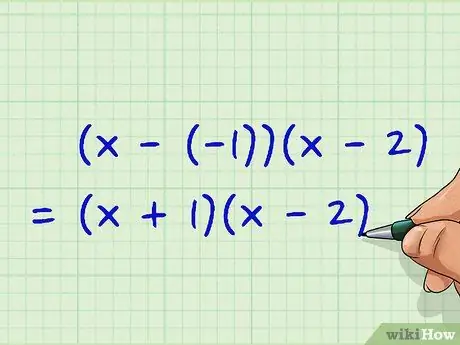
Step 4. Enter the previously obtained x values in the two factored expressions

If we call our two values of x 'h' and 'k', the expression we will use will be: (x - h) (x - k) = 0 So, our two factors must be: (x - (-1)) (x - 2) = (x + 1) (x - 2)

Advice

• If you have a TI-84 calculator, there is a program called SOLVER that can solve a quadratic equation. He will be able to solve polynomials of any degree.

• The coefficient of a non-existent term is 0. If this is the case, it may be useful to rewrite the equation.

  x² + 6 = x² + 0x + 6

• If you factored a polynomial using the quadratic formula and the result contains a radical, you could convert the values of x to fractions to verify the result.

• If a term does not have a coefficient, it is implied 1.

  x² = 1x²

• Eventually, you will learn to try mentally. Until then, it will be best to do it in writing.