An algebraic expression is a mathematical formula that contains numbers and / or variables. Although it cannot be solved since it does not contain the "equal" sign (=), it can be simplified. However, it is possible to solve algebraic equations, which contain algebraic expressions separated by the "equal" sign. If you want to know how to master this math concept, read on.
Steps
Part 1 of 2: Knowing the Basics
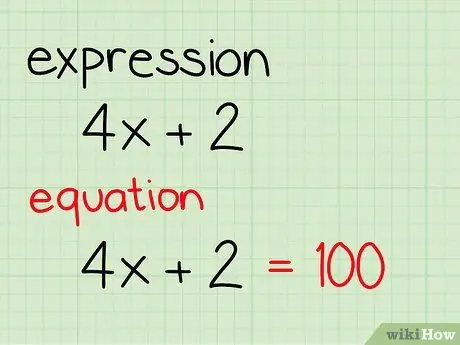
Step 1. Try to understand the difference between algebraic expression and algebraic equation
An algebraic expression is a mathematical formula that contains numbers and / or variables. It does not contain an equality sign and cannot be resolved. An algebraic equation, on the other hand, can be solved and contains a series of algebraic expressions separated by an equal sign. Here are some examples:
- Algebraic expression: 4x + 2
- Algebraic equation: 4x + 2 = 100
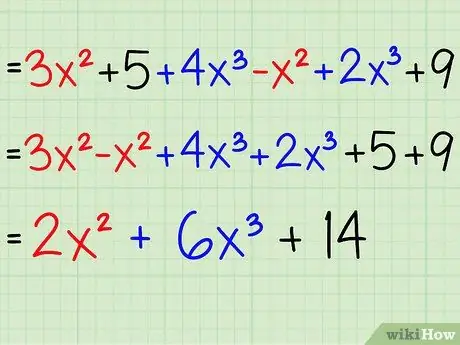
Step 2. Understand how to combine similar terms
Combining similar terms simply means adding (or subtracting) terms of equal rank. This means that all elements x2 can be combined with other x elements2, that all terms x3 can be combined with other x terms3 and that all constants, numbers that are not related to any variable, such as 8 or 5, can also be added or combined. Here are some examples:
- 3x2 + 5 + 4x3 - x2 + 2x3 + 9 =
- 3x2 - x2 + 4x3 + 2x3 + 5 + 9 =
- 2x2 + 6x3 + 14
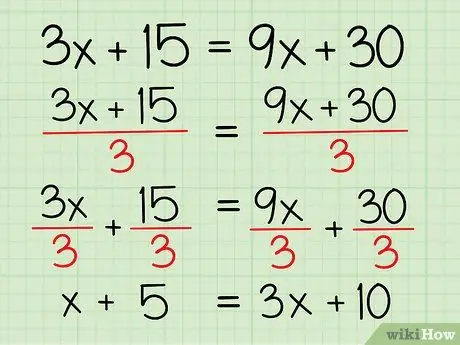
Step 3. Understand how to factor a number
If you are working on an algebraic equation, that is, you have an expression for each side of the equality sign, then you can simplify it using a common term. Look at the coefficients of all the terms (the numbers preceding the variables, or constants) and check if there is a number that you can "eliminate" by dividing each term by that number. If you can do it, you can also simplify the equation and start solving it. That's how:
-
3x + 15 = 9x + 30
Each coefficient is divisible by 3. Just "eliminate" the factor 3 by dividing each term by 3 and you will have simplified the equation
- 3x / 3 + 15/3 = 9x / 3 + 30/3
- x + 5 = 3x + 10

Step 4. Understand the order in which to carry out the operations
The order of operations, also known by the acronym PEMDAS, explains the sequence in which the mathematical operations must be carried out. The order is: P.arentesi, ANDsponents, M.oltiplication, D.vision, TOdiction e S.obtaining. Here is an example of how it works:
- (3 + 5)2 x 10 + 4
- First comes P and then the operation in brackets:
- = (8)2 x 10 + 4
- Then there is E and then the exponents:
- = 64 x 10 + 4
- Then we move on to multiplication:
- = 640 + 4
- And lastly the addition:
- = 644

Step 5. Learn to isolate variables
If you are solving an algebraic equation, then your goal is to have the variable, usually indicated with the letter x, on one side of the equation, and all the constants on the other. You can isolate the variable by division, multiplication, addition, subtraction, by finding the square root or by other operations. Once x is isolated, you can solve the equation. That's how:
- 5x + 15 = 65
- 5x / 5 + 15/5 = 65/5
- x + 3 = 13
- x = 10
Part 2 of 2: Solving an Algebraic Equation
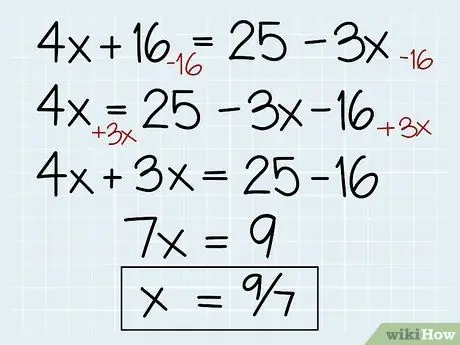
Step 1. Solve a simple linear algebraic equation
A linear algebraic equation contains only constants and variables of the first degree (no exponents or strange elements). To solve it we simply use multiplication, division, addition and subtraction to isolate and find x. Here's how it goes:
- 4x + 16 = 25 -3x
- 4x = 25 -16 - 3x
- 4x + 3x = 25 -16
- 7x = 9
- 7x / 7 = 9/7
- x = 9/7
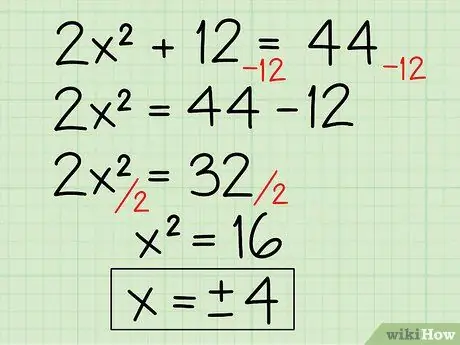
Step 2. Solve an algebraic equation with exponents
If the equation has exponents, then all you have to do is find a way to isolate the exponent from a part of the equation and then solve it by "removing" the exponent itself. Like? Finding the root of both the exponent and the constant on the other side of the equation. Here's how to do it:
-
2x2 + 12 = 44
First, subtract 12 from both sides:
- 2x2 + 12 -12 = 44 -12
-
2x2 = 32
Then, divide by 2 on both sides:
- 2x2/2 = 32/2
-
x2 = 16
Solve by extracting the square root on both sides in order to transform x2 in x:
- √x2 = √16
- Write down both results: x = 4, -4
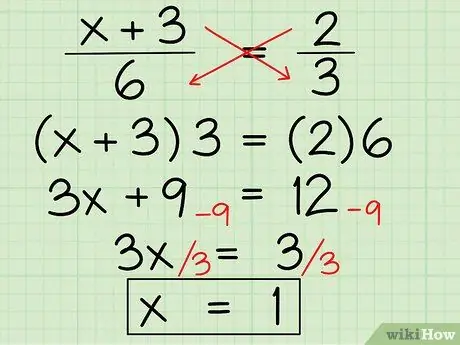
Step 3. Solve an algebraic expression containing fractions
If you want to solve an algebraic equation of this type you have to cross-multiply the fractions, combine similar terms and then isolate the variable. Here's how to do it:
-
(x + 3) / 6 = 2/3
First, do a cross-multiplication to eliminate the fraction. You have to multiply the numerator of one by the denominator of the other:
- (x + 3) x 3 = 2 x 6
-
3x + 9 = 12
Now combine the similar terms. Combine the constants, 9 and 12, by subtracting 9 from both sides:
- 3x + 9 - 9 = 12 - 9
-
3x = 3
Isolate the variable, x, by dividing both sides by 3 and you have the result:
- 3x / 3 = 3/3
- x = 3
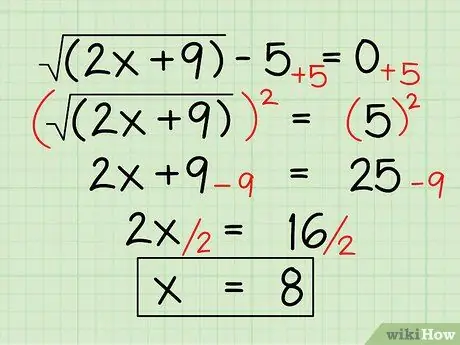
Step 4. Solve an algebraic expression with the roots
If you are working on an equation of this type, all you have to do is find a way to square both sides in order to eliminate the roots and find the variable. Here's how to do it:
-
√ (2x + 9) - 5 = 0
First, move everything that is not under the root to the other side of the equation:
- √ (2x + 9) = 5
- Then square both sides to remove the root:
- (√ (2x + 9))2 = 52
-
2x + 9 = 25
At this point, solve the equation as you normally would, combining the constants and isolating the variable:
- 2x = 25 - 9
- 2x = 16
- x = 8

Step 5. Solve an algebraic expression that contains absolute values
The absolute value of a number represents its value regardless of the "+" or "-" sign preceding it; the absolute value is always positive. So, for example, the absolute value of -3 (also written | 3 |) is simply 3. To find the absolute value, you have to isolate the absolute value and then solve twice for x. The first, simply by removing the absolute value and the second with the terms on the other side of the equal changed in sign. Here's how to do it:
- Solve by isolating the absolute value and then remove it:
- | 4x +2 | - 6 = 8
- | 4x +2 | = 8 + 6
- | 4x +2 | = 14
- 4x + 2 = 14
- 4x = 12
- x = 3
- Now solve again by changing the sign of the terms on the other side of the equation after having isolated the absolute value:
- | 4x +2 | = 14
- 4x + 2 = -14
- 4x = -14 -2
- 4x = -16
- 4x / 4 = -16/4
- x = -4
- Write down both results: x = -4, 3
Advice
- To cross-check the results, visit wolfram-alpha.com. It provides the result and often the two steps as well.
- Once you're done, replace the variable with the result and solve the sum to see if what you did makes sense. If so, congratulations! You have just solved an algebraic equation!






