In algebra, data inversion operations are often used to simplify the initial problem, which would otherwise be very complex to solve. For example, if you are required to perform division with a fractional value, it is much easier to multiply with its reciprocal. In this case, a reverse operation is performed. This concept applies very well to arrays, since division is not a valid operation in this area, so you solve the problem by performing a multiplication using inverse arrays. To find the inverse of a 3x3 matrix, a large amount of calculations have to be done manually, which may seem like a tedious job, but it is worth doing to discover the underlying concepts. Either way, you can take advantage of an advanced graphing calculator that will do all the work in moments.
Steps
Method 1 of 3: Calculate the Inverse Using the Added Matrix
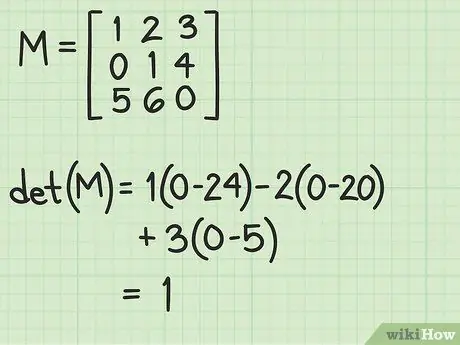
Step 1. Check the value of the determinant of the matrix under consideration
To find out if the matrix you are studying is invertible, you must first calculate its determinant. If the determinant is equal to 0, it means that your work is already finished because the matrix in question does not have an inverse. The determinant of a matrix M is indicated by the mathematical expression det (M).
- To calculate the determinant of a 3x3 matrix, you must first select a specific row or column, then calculate the lesser of each element of the chosen row or column and add the results obtained respecting the algebraic sign.
- For more details on how to calculate the determinant of a matrix, refer to this article.
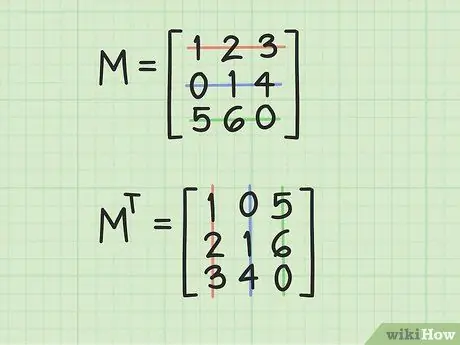
Step 2. Calculate the transpose of the original matrix
This step involves rotating the matrix 180 ° along the main diagonal. In other words, it means inverting the positional indices of each element of the array. For example, the element occupying position (i, j) will occupy position (j, i) and vice versa. When transposing the elements of a matrix, you notice that the main diagonal (the one that starts from the upper left corner and ends in the lower right corner) remains unchanged.
It is possible to think of the process of transposing a matrix as the operation that involves swapping rows with columns. The first row then becomes the first column, the middle row becomes the middle column, and the third row becomes the third column. Look at the image accompanying this step to graphically understand how the elements of the matrix under examination have changed their position after transposition

Step 3. Compute the minor of each element of the transposed matrix
The minor represents the determinant of the 2x2 matrix obtained by deleting the row and column to which a specific element belongs. Every number, variable or expression in a 3x3 matrix is associated with a 2x2 matrix whose determinant is called "minor" precisely because it refers to a smaller set of data. Once you have chosen an element and eliminated all those belonging to the same row and column, you get a 2x2 matrix to calculate the lesser of.
- In the example shown in the previous steps, if you want to calculate the minor of the element that is on the second row of the first column, you have to eliminate from the calculation all the elements that are part of the first column and the second row of the matrix. The determinant of the remaining 2x2 matrix represents the minor of the chosen element.
- Calculate the minor of each element belonging to the selected row or column by performing the operations and calculations shown so far in this section of the article.
- For more information on how to handle 2x2 matrices, please refer to this article.
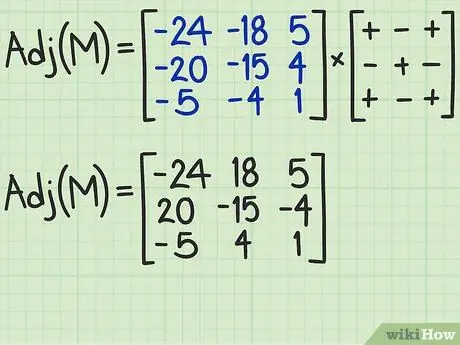
Step 4. Create the cofactor matrix (also known as the algebraic complement matrix)
Place the results obtained in the previous step inside a new matrix, called cofactors, by inserting the minor of each element in the relative position of the original matrix. For example, the minor of the element (1, 1) of the original matrix will be placed in the same position of the cofactor matrix. At this point, modify the algebraic sign of each element of the new matrix by multiplying it by the sign shown in the same position of the reference matrix that you find inside the figure accompanying the passage.
- When you do this, the first element of the first row of the array keeps its original sign, the second element will have its sign reversed while the third will keep its original sign again. Continue processing the rest of the elements of subsequent lines using this pattern. Note that the signs "+" and "-", which you find in the reference matrix, do not indicate the algebraic sign that the relative element of the cofactor matrix must have, but simply that the relative element must have the inverted sign (indicated by the symbol "-") or keep the original one (indicated by the "+" symbol).
- For more information on how to get the cofactor matrix of a given matrix, see this article.
- The resulting matrix from this step is called the added matrix of the original matrix. The added matrix is indicated by the mathematical expression adj (M).

Step 5. Divide each element of the added matrix by the determine
The latter is the determinant of the starting matrix M that we calculated in the first steps to find out if it was possible to invert it. Divide each value of the added matrix by the determinant. Places the result obtained from each calculation in place of the relative element of the added matrix. The resulting new matrix represents the inverse of the original M matrix.
- For example, the determinant of the reference matrix for this section, shown in the related images, is equal to 1. Dividing each element of the added matrix by the determinant will then result in the added matrix itself (in this case we were lucky, but not it is always so unfortunately).
- Regarding this last step, instead of performing the division, other sources multiply each element of the added matrix by the inverse of the determinant of the original matrix, that is 1 / det (M). Mathematically speaking, the two operations are equivalent.
Method 2 of 3: Find the Inverse Matrix via Line Reduction
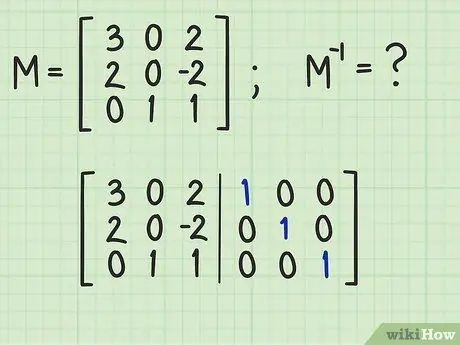
Step 1. Add the identity matrix to the original matrix
Make a note of the original matrix, draw a vertical dividing line to its right, then write the identity matrix to the right of the line just drawn. You should now have a matrix consisting of 3 rows and 6 columns.
Remember that the identity matrix is a special matrix, made up of elements that take the value 1 arranged along the entire main diagonal and of elements that take the value 0 in all other positions. Search online for more information about the identity matrix and its properties
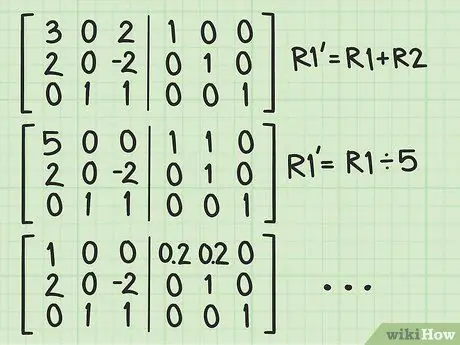
Step 2. Perform the row reduction of the new matrix obtained
The goal is to be able to move the identity matrix from the right side to the left side of the new matrix. By performing the operations inherent to the reduction by rows on the left side of the matrix, you will have to apply them also to the right side, so that it begins to take the form of an identity matrix.
Remember that the row reduction of a matrix is performed through a combination of scalar multiplications and additions or subtractions in order to bring to 0 the elements that are below the main diagonal of the reference matrix. For more detailed information on how to perform row reduction of a matrix, search the web
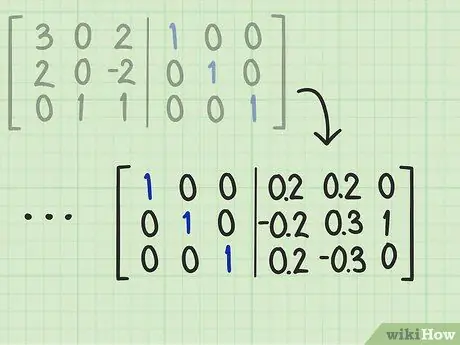
Step 3. Continue your calculations until you get an identity matrix on the left side of the starting matrix
Continue by performing the mathematical operations required to reduce the starting matrix until the left side exactly reflects the identity matrix (consisting of 1 on the main diagonal and 0 in all other positions). Once you reach the goal, on the right side of the vertical dividing line, you will have exactly the inverse of the original matrix.
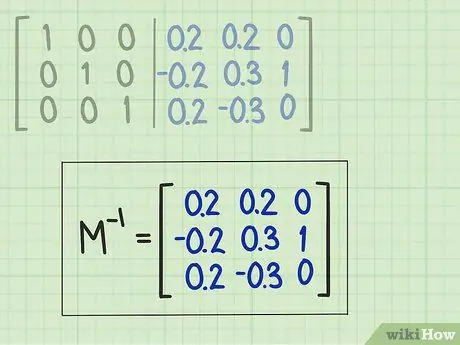
Step 4. Make a note of the inverse matrix
Copies all the elements that appear on the right side of the vertical dividing line of the starting matrix into the inverse matrix.
Method 3 of 3: Use a Calculator to Find the Inverse Matrix

Step 1. Choose a calculator model that can process matrices
The normal calculators used to perform the 4 basic mathematical operations will not help you with this method. In this case you need to use a scientific calculator with advanced graphing capabilities, such as the Texas Instruments TI-83 or TI-86, which can greatly reduce your workload.

Step 2. Enter the values of the elements of the matrix into the calculator
If your calculator is equipped with it, press the "Matrix" button to activate the calculation mode related to the management of matrices. If you are using a calculator made by Texas Instruments, you must press the key combination "2nd"and" Matrix ".

Step 3. Enter the "Edit" submenu
To reach this menu, you may need to use the arrow keys or choose the appropriate function key combination, depending on the make and model of your calculator.

Step 4. Choose one of the available matrices
Most calculators are designed to handle 3 to 10 matrices, labeled with the letters of the English alphabet from A to J, respectively. Normally, for simplicity, you choose to use matrix [A]. After making your selection, press the "Enter" key.

Step 5. Enter the dimensions of the matrix to be processed
In this article we focus on 3x3 matrices. However, a normal graphing calculator can also handle much larger matrices. Type the number of rows that make up the matrix, then press the "Enter" key, then type the number of columns and press the "Enter" key again.

Step 6. Enter the elements that make up the matrix
A matrix will appear on the calculator screen. If you have previously used the "Matrix" function of the device, the last matrix you worked with will appear on the screen. The cursor is positioned on the first element of the matrix. Enter the value of the elements of the matrix you need to work on, then press the "Enter" key. The cursor will automatically move to the next item to type, overwriting its previous value in case you have already used the calculator to work with matrices in the past.
- If you need to enter a negative value, you must press the button relating to the negative sign ("-") and not the one relating to mathematical subtraction.
- To move the cursor within the matrix, you can use the directional keys of the device.

Step 7. Exit the "Matrix" operating mode
After typing in all the values of the elements that make up the matrix, press the "Quit" key (or use the key combination "2nd"and" Quit "). In this way the" Matrix "functionality will be deactivated and the main screen of the calculator will appear on the screen.

Step 8. To find the inverse matrix, press the appropriate key on the calculator
First, you need to select the matrix you want to work with, then you will have to activate the "Matrix" mode again and choose the name of the matrix you used to enter the data of the one you are working on (most likely it will be the matrix [A]). At this point, press the key to calculate the inverse matrix, x − 1 { displaystyle x ^ {- 1}}
. In some cases you will have to press the key first to activate the second function,
nd", depending on your calculator model. A − 1 { displaystyle A ^ {- 1}} should appear on the device screen
. By pressing the key">
- Do not use the calculator's "^" key when trying to type the "A ^ -1" command. It is still a simple scientific calculator, which does not include special commands other than those programmed and pre-installed by the manufacturer.
- If an error message appears after pressing the reverse key, it is very likely that the matrix you are inserting does not have an inverse. To verify this, you will need to calculate the relevant determinant.

Step 9. Convert the resulting inverse matrix into the correct form
The calculator will show the elements of the matrix in the form of decimal numbers. In most areas of mathematics this form is not considered "correct". If necessary, you will then have to convert all values to fractional numbers. In very rare, and very lucky cases, all elements of the matrix will appear in the form of integers.
Your calculator is most likely equipped with a function that can automatically convert decimal numbers to fractions. For example, if you are using the Texas Instruments TI-86 calculator, activate the "Math" function, access the "Misc" menu, choose the "Frac" function and finally press the "Enter" key. The decimal numbers will automatically be converted to fractions
Advice
- You can also use the steps described in this article to calculate the inverse of a matrix that contains numbers, variables, data of an unknown nature, or algebraic expressions.
- Do the calculations in writing, as calculating the inverse of a 3x3 matrix in mind is extremely complex.
- Existing programs are able to instantly calculate the inverse of very large matrices with a size up to 30x30..
- Always check that the results obtained are correct, regardless of the method used. To do this, multiply the original matrix by the inverse matrix (M x M-1). Check that the following expression is true: M * M-1 = M-1 * M = I. I represents the identity matrix which is composed of elements with a value of 1 along the main diagonal and of elements of 0 in all other positions. If you get a different result, it means that you have made some calculation errors in some step.






