A system of equations is a system of two or more equations, which has a set of shared unknowns and therefore a common solution. For linear equations, which are graphed as straight lines, the common solution in a system is the point where the lines intersect. Arrays can be useful for rewriting and solving linear systems.
Steps
Part 1 of 2: Understanding the Basics

Step 1. Know the terminology
Linear equations have distinct components. The variable is the symbol (usually letters like x and y) that stands for a number you don't know yet. The constant is a number that remains consistent. The coefficient is a number that comes before a variable, which is used to multiply it.
For example, in the linear equation 2x + 4y = 8, x and y are variables. The constant is 8. The numbers 2 and 4 are coefficients
Step 2. Recognize the shape for a system of equations
A system of equations can be written as follows: ax + by = pcx + dy = q Each of the constants (p, q) can be null, with the exception that each of the two equations must contain at least one of the two variables (x, y).
Step 3. Understanding Matrix Equations
When you have a linear system, you can use a matrix to rewrite it, then use the algebraic properties of that matrix to solve it. To rewrite a linear system, use A to represent the coefficient matrix, C to represent the constant matrix, and X to represent the unknown matrix.
The previous linear system, for example, can be rewritten as an equation of matrices as follows: A x X = C
Step 4. Understand the concept of augmented matrix
An augmented matrix is a matrix obtained by tiling the columns of two matrices, A and C, which looks like this You can create an augmented matrix by tiling them. The augmented matrix will look like this:
-
For example, consider the following linear system:
2x + 4y = 8
x + y = 2
Your augmented matrix will be a 2 x 3 matrix that has the appearance shown in the figure.
Part 2 of 2: Transform the Augmented Matrix to Fix the System

Step 1. Understand the elementary operations
You can perform some operations on a matrix to transform it while keeping it equivalent to the original. These are called elementary operations. To solve a 2x3 matrix, for example, you can use elementary operations between rows to transform the matrix into a triangular matrix. Elementary operations include:
- exchange of two lines.
- multiplying a row by a non-zero coefficient.
- multiply a row and then add it to another.
Step 2. Multiply the second row by a non-zero number
You want to have a zero in your second row, so multiply it to get the desired result.
For example, let's say you have a matrix like the one in the figure. You can keep the first row and use it to get a zero in the second. To do this, multiply the second row by two, as shown in the figure
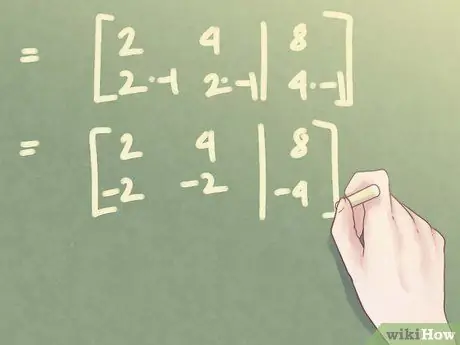
Step 3. Continue multiplying
To get a zero for the first row, you may need to multiply again, using the same principle.
In the example above, multiply the second row by -1, as shown in the figure. When you have finished multiplying the matrix should look similar to that of the figure
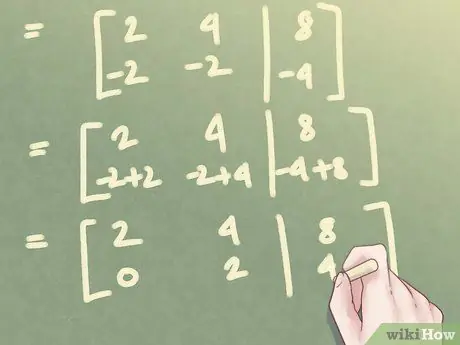
Step 4. Add the first row with the second
Then, add the first and second rows to get a zero in the first column of the second row.
In the example above, add the first two lines as shown in the figure
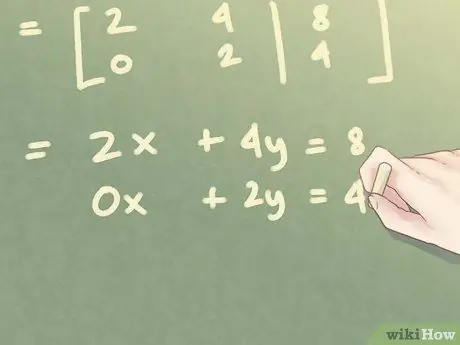
Step 5. Write the new linear system starting from the triangular matrix
At this point, you have a triangular matrix. You can use that matrix to get a new linear system. The first column corresponds to the unknown x, and the second column to the unknown y. The third column corresponds to the member with no unknowns of the equation.
In the example above, the system will look as shown in the figure
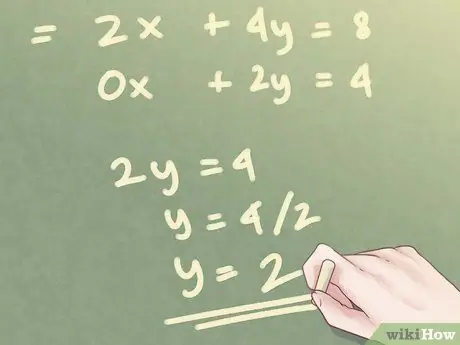
Step 6. Solve for one of the variables
Using your new system, determine which variable can be easily determined, and solve for that.
In the example above, you want to solve "backwards": starting from the last equation to the first to solve for your unknowns. The second equation gives you a simple solution for y; since z has been removed, you can see that y = 2
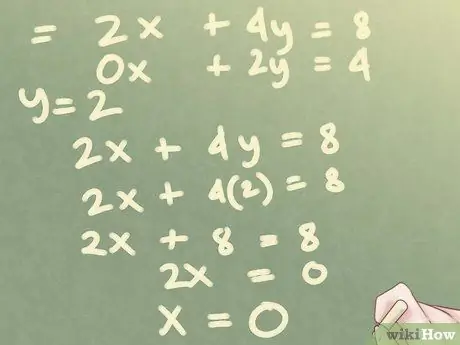
Step 7. Substitute to solve for the first variable
Once you have determined one of the variables, you can substitute that value in the other equation to solve for the other variable.
In the example above, replace y with a 2 in the first equation to solve for x, as shown in the figure
Advice
- The elements arranged within a matrix are usually called "scalars."
- Remember that to solve a 2x3 matrix, you have to stick to the elementary operations between the rows. You cannot perform operations between columns.






