Spearman's Coefficient of Correlation for Ranks allows you to identify the degree of correlation between two variables in a monotone function (for example, in the case of a proportional or proportionally inverse increase between two numbers). Follow this simple guide to manually calculate, or know how to calculate, the correlation coefficient in Excel or the R program.
Steps
Method 1 of 3: Manual Calculation
Step 1. Create a table with your data
This table will organize the information needed to calculate Spearman's Rank Correlation Coefficient. You will need:
- 6 columns, with headings as shown below.
- As many lines as there are pairs of data available.
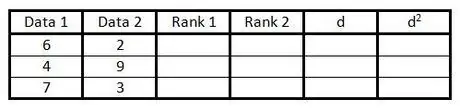
Step 2. Fill in the first two columns with your data pairs
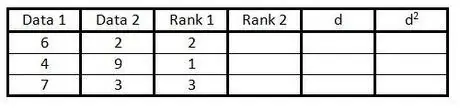
Step 3. In the third column classify the data in the first column from 1 to n (the number of data available)
Rank the lowest number with rank 1, the next lowest number with rank 2, and so on.
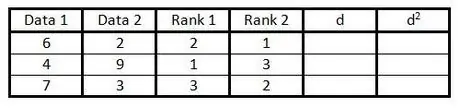
Step 4. Operate on the fourth column as in step 3, but rank the second column instead of the first
-

Mean_742 If two (or more) data in a column are identical, find the rank mean, as if the data were ranked normally, then rank the data using this mean.
In the example on the right, there are two 5s that would theoretically have a rank of 2 and 3. Since there are two 5s, use the average of their ranks. The average of 2 and 3 is 2.5, so assign rank 2.5 to both numbers 5.
Step 5. In column "d" calculate the difference between the two numbers in each pair of ranks
That is, if one of the numbers is ranked in rank 1 and the other in rank 3, the difference between the two would result in 2. (The sign of the number does not matter, since in the next step this value will be squared).
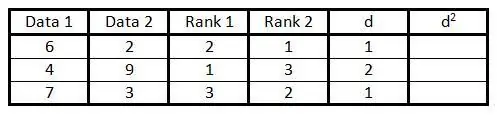
Step 6.
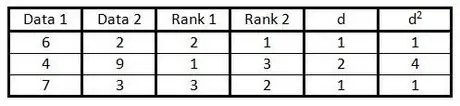
Step 7. Square each of the numbers in column "d" and write these values in column "d2".
Step 8. Add all the data in column d2".
This value is represented by Σd2.
Step 9. Enter this value into the Spearman Rank Correlation Coefficient formula
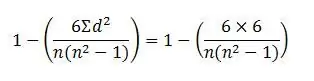
Step 10. Replace the letter "n" with the number of data pairs available, and calculate the answer
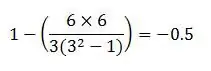
Step 11. Interpret the result
It can vary between -1 and 1.
- Close to -1 - Negative correlation.
- Close to 0 - No linear correlation.
- Close to 1 - Positive correlation.
Method 2 of 3: In Excel
Step 1. Create new columns with the ranks of existing columns
For example, if the data is in column A2: A11, you will use the formula "= RANK (A2, A $ 2: A $ 11)", copying it to all rows and columns.
Step 2. In a new cell, create a correlation between the two columns of the rank with a function similar to "= CORREL (C2: C11, D2: D11)"
In this case, C and D would correspond to the rank columns. The correlation cell will provide the Spearman rank correlation.
Method 3 of 3: Using Program R
Step 1. If you don't already have it, download the R program
(See
Step 2. Save the contents in a CSV file with the data you want to relate in the first two columns
Click on the menu and choose "Save As".
Step 3. Open the R program
If you are on the terminal, it will be sufficient to run R. On the desktop, click on the program logo R.
Step 4. Type the commands:
- d <- read.csv ("NAME_OF_TUO_CSV.csv") and press enter
- correlation (rank (d [, 1]), rank (d [, 2]))
Advice
Most of the data should contain at least 5 data pairs to identify a trend (3 data pairs were used in the example to make it easier to demonstrate)
Warnings
- The Spearman Correlation Coefficient will only identify the degree of correlation where there is a constant increase or decrease in the data. If using a data scatter plot, the Spearman coefficient Not will provide an accurate representation of this correlation.
- This formula is based on the assumption that there are no correlations between variables. When there are correlations like the one shown in the example, you need to use Pearson's rank-based correlation index.






