4 Ways to Calculate Derivatives in Mathematical Analysis

2024 Author: Samantha Chapman | [email protected]. Last modified: 2023-12-17 09:13

Derivatives can be used to obtain the most interesting characteristics of a graph, such as highs, lows, peaks, valleys and slopes. It's even possible to draw complex equations without a graphing calculator! Unfortunately, getting the derivative is often boring, but this article will help you with some tips and tricks.

Steps

Step 1. Try to understand the notation of the derivative

The following two notations are the most common, although there are countless others:

• Leibniz notation: This notation is more common when the equation involves y and x.

  dy / dx literally means "the derivative of y with respect to x". It may be useful to think of the derivative as Δy / Δx for values of x and y that are infinitesimally different from each other. This explanation is suitable for the definition of limit of a derivative:

  lim _{h-> 0} (f (x + h) - f (x)) / h.

  When using this notation for the second derivative, you must write:

  dy² / right².

• Lagrange notation: the derivative of a function f is also written as f '(x). This notation is pronounced "f prime of x". This notation is shorter than Leibniz's and is useful when looking for the derivative of a function. To form the derivatives of higher order, just add another sign "'" and so the second derivative becomes f "(x).

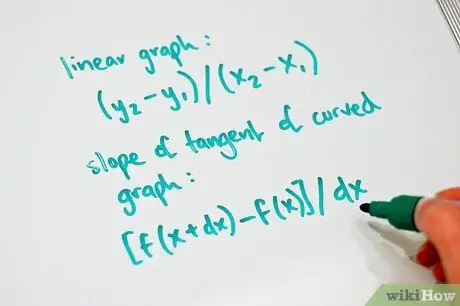
Step 2. Try to understand what the derivative is and why it is used

First of all, to find the slope of a linear graph, we take two points on the line and their coordinates that we insert into the equation (y₂ - y₁) / (x₂ -x₁). However, this can only be used with line charts. For quadratic and higher degree equations, the line is curved, so it is not accurate to take the "difference" of the two points. In order to find the slope of the tangent of a curve graph, we take two points and connect them with the standard equation to find the slope of the graph of a curve: [f (x + dx) - f (x)] / right. DX stands for "delta x", which is the difference between the two x coordinates of the two points on the graph. Note that this equation is the same as (y₂ - y₁) / (x₂ - x₁), but it's just in a different form. Since it is already known that the result will be inaccurate, an indirect approach is applied. To find the slope of the tangent in the generic point with coordinates (x, f (x)), dx must approach 0, so that the two points that have been taken "merge" into a single point. However, it is not possible to divide by 0, so after substituting the coordinate values of the two points, you will need to use factorization and other methods to simplify the right to the denominator of the equation. Once done, set dx tending to 0 and solve. This is the slope of the tangent at the coordinate point (x, f (x)). The derivative of an equation is the generic equation for finding the slope or angular coefficient of any line tangent to a graph. This may sound very complicated, but there are a few examples below, which will help clarify how to obtain the derivative.

Method 1 of 4: Explicit Derivation

Step 1. Use explicit derivation when the equation already has y on one side of the equality

Step 2. Enter the equation of the formula [f (x + dx) - f (x)] / dx

For example, if the equation is y = x², the derivative becomes [(x + dx) ² - x²] / right.

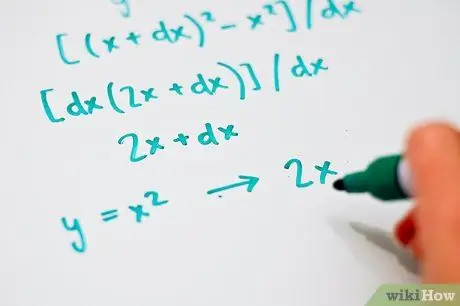
Step 3. Multiply and then collect dx to form the equation [dx (2 x + dx)] / dx

Now it is possible to simplify dx between numerator and denominator. The result is 2 x + dx and, when dx approaches 0, the derivative is 2x. This means that the slope of each tangent of the graph y = x ² is 2x. Just replace the value of x with the abscissa of the point where you want to find the slope.

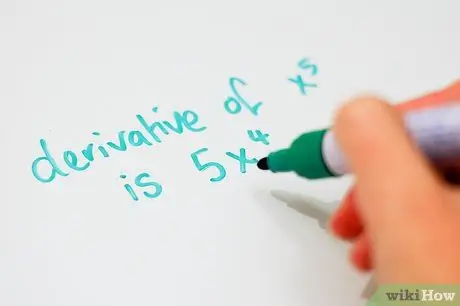
Step 4. Learn patterns for deriving similar type equations

Here are a few.

• The derivative of any power is the denominator of the power multiplied by x raised to the power value minus 1. For example, the derivative of x⁵ is 5x⁴ and the derivative of x^{3, 5} is 3.5x^{2, 5}. If there is already a number in front of the x, just multiply it by the exponent of the power. For example, the derivative of 3x⁴ is 12x³.
• The derivative of a constant is zero. Thus the derivative of 8 is 0.
• The derivative of a sum is the sum of its individual derivatives. For example, the derivative of x³ + 3x² is 3x² + 6x.
• The derivative of a product is the derivative of the first factor for the second plus the derivative of the second for the first. For example the derivative of x³(2 x + 1) is x³(2) + (2 x + 1) 3x², equal to 8x³ + 3x².
• And finally the derivative of a quotient (i.e. f / g) is [g (derivative of f) - f (derivative of g)] / g². For example the derivative of (x² + 2x - 21) / (x - 3) is (x² - 6x + 15) / (x - 3)².

Method 2 of 4: Implicit Derivation

Step 1. Use the implicit derivation when the equation cannot be written easily with y on only one side of the equality

Even if you were able to write with y on one side, the calculation of dy / dx would be boring. Below is an example of how this type of equation might be solved.

Step 2. In this example, x²y + 2y³ = 3x + 2y, replace y with f (x), so you will remember that y is actually a function.

So the equation becomes x [f (x)]² + 2 [f (x)]³ = 3x + 2f (x).

Step 3. To find the derivative of this equation, differentiate (a big word to find the derivative) both sides of the equation with respect to x

So the equation becomes x²f '(x) + 2xf (x) + 6 [f (x)]²f '(x) = 3 + 2f' (x).

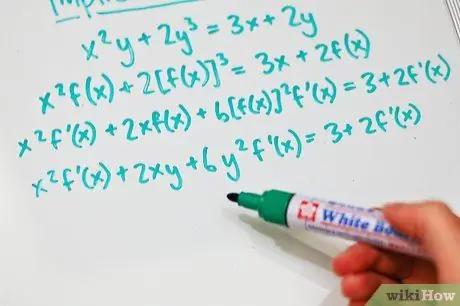
Step 4. Replace f (x) again with y

Be careful not to do the same with f '(x), which is different from f (x).

Step 5. Solve for f '(x)

The answer for this example is (3 - 2xy) / (x ² + 6y ² - 2).

Method 3 of 4: Derivatives of a Higher Order

Step 1. Making a higher order derivative of a function only means making the derivative of the derivative (for order 2)

For example, if you are asked to calculate the third order derivative, just do the derivative of the derivative of the derivative. For some equations, the higher order derivatives make 0.

Method 4 of 4: The Chain Rule

Step 1. When y is a differentiable function of z, z is a differentiable function of x, y is a composite function of x and the derivative of y with respect to x (dy / dx) is (dy / du) * (du / dx)

The chain rule can also be valid for compound power (power of power) equations, like this: (2x⁴ - x)³. To find the derivative, just think of the product rule. Multiply the equation by the power and decrease the power by 1. Then multiply the equation by the derivative of the inner part of the power (in this case, 2x⁴ - x). The answer to this question comes 3 (2x⁴ - x)²(8x³ - 1).

Advice

• The derivative of yz (where y and z are both functions) is not simply 1, because y and z are separate functions. Use the product rule: yz = y (1) + z (1) = y + z.
• Practice the product rule, the quotient rule, the chain rule and above all the implicit derivation, as these are by far the most difficult in differential analysis.
• Whenever you see a huge problem to solve, don't worry. Just try to break it into very small pieces by applying the product standards, quotient etc. Then it derives the individual parts.
• Get to know your calculator well - test different functions of your calculator to learn how to use them. It is particularly useful to know how to use the tangent and derivative functions of your calculator, if they exist.
• Memorize the basic derivatives of trigonometry and learn how to manipulate them.