The first thing to understand is that they are there two main categories of percentage problems: direct comparison questions (such as "35 is 5% of what number"?) e requests for increase / decrease (like, "if a blouse that costs $ 45 is originally on sale at 20% off, what's the new price?"). The increment / decrement type of problems is complicated enough to require a separate wikiHow article, so let's just focus on direct comparison for now.
The other thing to know is that there are two main approaches to these problems. One is based on an equation that requires decimals, and the other is based on proportions. I am going to describe the method which is based on the equation with decimals, which is: % x (total quantity) = (partial quantity). This equation can be rewritten like this: % = (partial quantity) / (total quantity). It can also be written like this: (total quantity) = (partial quantity) /%. Which of these forms of the equation is needed depends on what kind of problem you have.
Where to start
Your first task is understand what kind of problem you are facing. In a situation of direct confrontation, they are there three types of problems. In first type "the percentage" is the data to be found. Problems of this type are expressed like this: "what percentage of 25 is 16?" or "8 what percentage is 32?". In second type "the total quantity" is the data to be found. Problems of this type are expressed in this way: "15 is 6% of what number?" or "78% of which number is 20?". In third type "the partial quantity" is the data to be found, and the questions will be expressed like this: "What is 52% of 49?" or "14% of 225 how much is it?"
Steps
Method 1 of 3: Find the "Percent"
If you don't see a number with a% sign (or possibly the word "percent"), this is almost certainly a problem where "percentage" is the data to find.
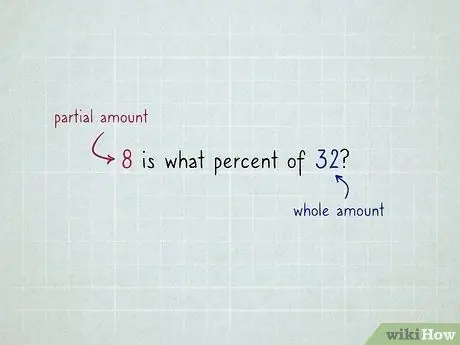
Step 1. Decide which of the other numbers is the "total amount" and which is the "partial amount"
For example, a problem that says "8 what percentage is 32?" indicates that 32 is the total quantity and 8 is the partial quantity. This suggests some clues: 8 connects directly to "is", while 32 connects directly to "di".

Step 2. Use the equation% = (partial) / (total)
So on the calculator, type the partial quantity, hit the division symbol, enter the integer quantity, and hit the equal symbol.

Step 3. The equation will give you a decimal number, which you will convert into a percentage by moving the decimal point two places to the right
-
Example: "8 what percentage is 32?". Take 8, divide by 32, hit equal; you get 0.25; convert this to 25%.

Work With Percentages Step 3Bullet1 -
Example: "what percentage of 25 is 16?". Enter 16, divide by 25, press equal; you get 0, 64; converted to 64%.

Work With Percentages Step 3Bullet2 -
Example: "what percentage of 12 is 45?". Enter 45, divide by 12, press equal; you get 3.75; converted into 375%. (Answers above 100% are rare, but acceptable).

Work With Percentages Step 3Bullet3 -
Example: "9 what percentage is 250?". Enter 9, divide by 250, press equal; you get 0, 036; converted into 3, 6%.

Work With Percentages Step 3Bullet4
Method 2 of 3: Find the "Total Quantity"
Let's say you have a percentage. Now you have to decide if the data to find is the "total quantity" or the "partial quantity". This is a bit more complicated and a lot depends on the context of the application.

Step 1. Watch for the "is" and "of" and "which" markers
"Is" tends to be associated with the partial amount, while "of" is coupled with the full amount. The word "which" indicates the data to be found.
-
Example: A question says, "what is 10% of 16?" The expression "what is" indicates that the partial quantity is the data to be found. The phrase "of 16" indicates that 16 is the total quantity. This is an "unknown partial quantity" problem.

Work With Percentages Step 4Bullet1 -
Example: A question says, "15 is 25% of what number?" The phrase "of which" means that the total amount is unknown, but the phrase "15 is" indicates that 15 is the partial amount. This is an "unknown total quantity" problem.

Work With Percentages Step 4Bullet2

Step 2. Suppose you have an "unknown total amount" problem, such as "15 is 25% of what number?
. First of all, change the percentage to a decimal number - 0.25 instead of 25%, 1.38 instead of 138%, 0.07 instead of 7%, etc.

Step 3. Use the equation:
(total quantity) = (partial quantity) /%.
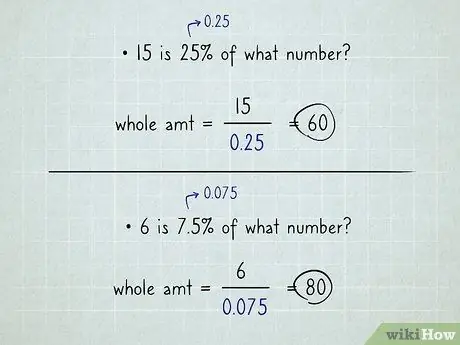
Step 4. Using the calculator, enter the partial quantity, press the division symbol, enter the decimal value of the percentage and press equal
-
Example: "15 is 25% of what number?". Take your calculator, enter 15, hit the division key, enter 0, 25, hit equal. The answer is 60. You are done. (Notice, the result is only 60. Not 60%).

Work With Percentages Step 7Bullet1 -
Example: "32% of which number is 16?". Enter 16, press the division key, enter 0, 32, press equal; the answer is 50.

Work With Percentages Step 7Bullet2 -
Example: "125% of which number is 80?". Enter 80, press the division key, enter 1, 25, press equal; the answer is 64.

Work With Percentages Step 7Bullet3 -
Example: "6 is 7.5% of what number?". Enter 6, press the division key, enter 0, 075, press equal; the answer is 80.

Work With Percentages Step 7Bullet4
Method 3 of 3: Find the "Partial Quantity"

Step 1. Look at the "is", "of" and "which" (or even "how much") indicators
If the "is" and the "which" are closely associated, as in the question "What is 10% of 16?", Then you have an "unknown partial quantity" problem.

Step 2. Here's what to do: Change the percentage back to a decimal number, so 32% is 0.32 and 75% is 0.75 and 150% is 1.5 and 6% is 0.06 and so on.

Step 3. Use the equation:
% x (total quantity) = (partial quantity). In other words, multiply the decimal number of the percentage by the total amount.
-
Example: "what is 10% of 16?". Enter 0, 10, press the key to multiply, enter 16, press equal. The answer is 1, 6 (note, there is no sign of% in the answer).

Work With Percentages Step 10Bullet1 -
Example: "What is 230% of 40?". Enter 2, 3, press the key to multiply, enter 40, press equal. The answer: 92.

Work With Percentages Step 10Bullet2 -
Example: "What is 37% of 200?". Enter 0, 37, press the key to multiply, enter 200, press equal. Answer: 74.

Work With Percentages Step 10Bullet3
Advice
-
The only time you need to multiply is if you have the% and the total amount.
In other cases you have to divide.
- With the "unknown partial quantity" problem, the order of multiplication does not matter. You could solve "230% of 45" with the sequence of 2, 3 x 45 =, or with 45 x 2, 3 =
- Apply the TLAR (That Looks About Right) principle --- the result looks right ---. Make sure your answer is reasonable.
- To summarize, you can: A) divide the partial quantity FOR the total quantity; or, B) divide the partial quantity FOR the percentage; or, C) multiply the total quantity by the percentage. Which of these to use depends on what numbers you have.
Warnings
- Order in the division is of vital importance! In both problems that are solved by division, the partial quantity must be entered into the calculator first.
- Most calculators have a percentage key. Its purpose is to move the decimal point two places to the left, changing 35% to 0, 35 and 325% to 3, 25 and 6% to 0, 06, and so on. I suggest you NOT use this key, because I have found that most students move the decimal point mentally, so if you press the% key as well, a big mess comes up.






