The abacus is a deceptively simple calculation tool that is still used around the world today. The suanpan, or Chinese abacus, is the most useful model; it is perfect for people with low vision and for anyone who wants to know the basic processes of modern calculators. After learning the fundamentals of counting with this tool, you can quickly perform arithmetic operations, such as division, addition, subtraction and multiplication.
Steps
Part 1 of 4: Counting
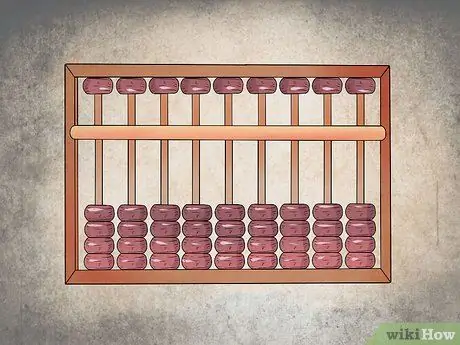
Step 1. Orient the schedule correctly
Each column of the upper sector must have one or two grains, while those of the lower sector should have four each. At the beginning, all the grains of the upper sector must be pushed upwards and those of the lower sector downwards; the upper grains represent five units, while the lower ones represent one unit each.
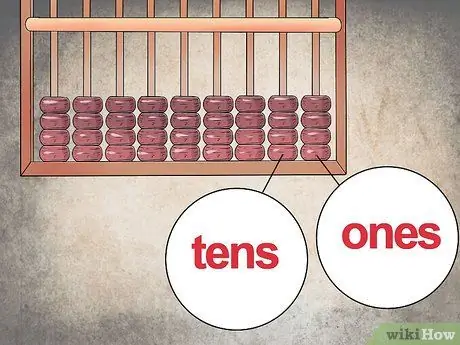
Step 2. Assign a positional value to each column
Just like in modern calculators, each column represents a "position" that allows you to construct the number. According to this logic, the far right column should contain the "units" (1-9), the second the "tens" (10-99), the third the "hundreds" (100-999) and so on.
- If necessary, you can also decide that some columns are decimals.
- For example, if you want to represent the number "10, 5", the far right column represents the first decimal place, the second the units and the third the tens.
- Similarly, to represent the number "10, 25" the last column on the right is assigned to the cents, the penultimate to the tenths, the third from the right to the units and finally the last to the tens.

Step 3. Start counting using the grains found in the lower sector
To count each digit, bring a bead to the top. The number "one" is represented by moving up one grain of the last column on the right, the number "two" by moving two grains and so on.
You may find that it is easier to use your thumb to raise the lower sector beads and your index finger to lower those of the upper sector
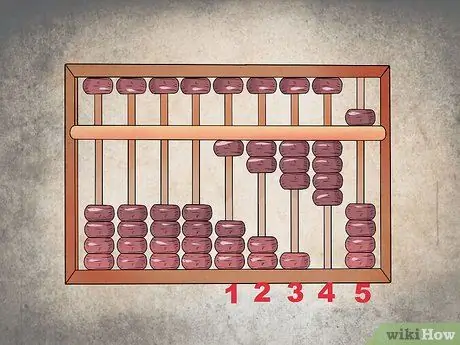
Step 4. Complete the step from "4" to "5"
Since there are only four beads in the lower sector, to go from number "4" to "5", you must lower one grain of the upper sector and return all the beads of the lower one to their original position. A schedule configured in this way correctly indicates the number "5". To represent the number "6", move one grain of the lower sector upwards; in this way, the one of the upper portion (indicating the "5") is at the bottom and one of those of the lower portion is at the top.
Step 5. Keep this criterion to indicate larger numbers
The process is essentially always the same and must be applied to all the columns of the abacus. It goes from number "9" - whereby all unit beads are pushed up and the top sector bead is pushed down - to "10" by bringing up one grain of the tens column and "zeroing "the unit column (the beads must be in the starting position).
- For example, to indicate the number "11", you have to push up one grain of the second column and one of the first column on the right (both of the lower sector); to configure the abacus in the "12" position, bring up one bead in the tens column and two in the units column.
- The number "226" has two raised beads in the third column from the right and two in the second column; in the first column (that of the units) bring down a bead from the upper sector and lift one from the lower one.
Part 2 of 4: Adding and Subtracting
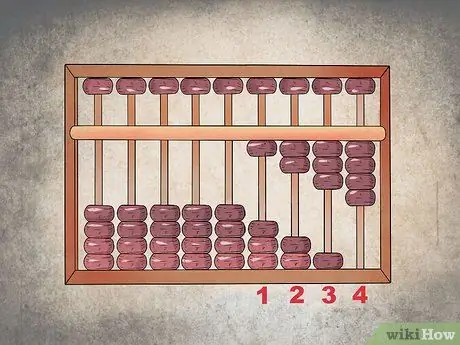
Step 1. Enter the first number
Suppose you need to add "1234" to "5678". First, configure the abacus to indicate "1234" by bringing up all four beads in the first column, three in the tens column, two in the hundreds, and one in the thousands column.
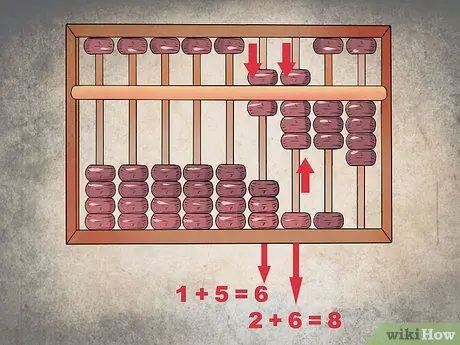
Step 2. Start adding from the left
The first two numbers you need to add are "1" and "5" in the thousands column; in this case, you just need to lower a grain of the upper sector to add "5", leaving the configuration of the lower sector unchanged in order to represent the "6". Similarly, to add the number "6" in the hundreds column, lower one grain from the upper sector and lift one from the lower sector to get the total of "8".
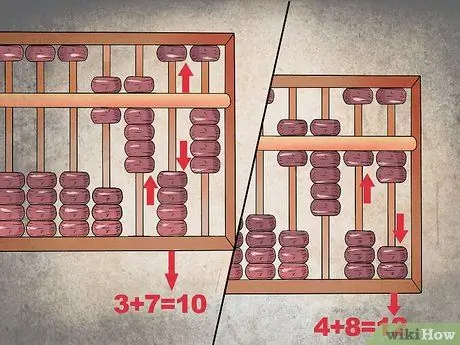
Step 3. Complete a trade
Since the addition in the tens column leads to the number "10", you must "put" the value "1" in the hundreds column, so that it indicates "9"; then, lower all the tens beads to clear the column.
As for the units column, you have to basically repeat the same thing. "8" plus "4" equals "12", so put a ten in the second column and configure the first to indicate the number "2"
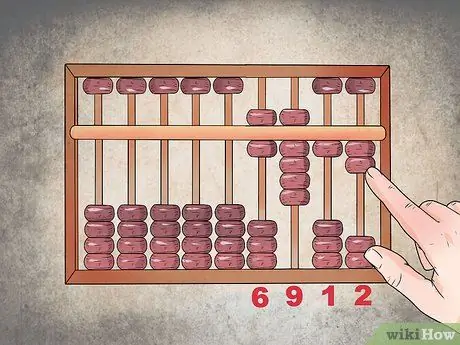
Step 4. Count the beads to get the solution
At this point, you have the number "6" in the thousands column, the "9" in the hundreds column, the tens indicate the number "1" and the units "2"; consequently: 1234 + 5678 = 6912.
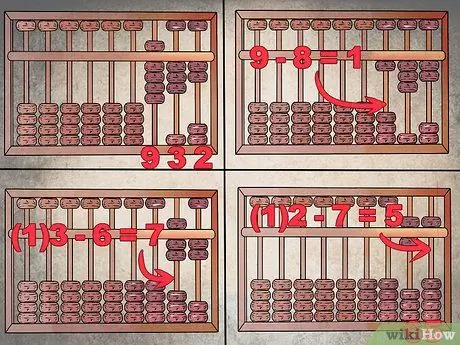
Step 5. Perform the subtraction following the reverse procedure
Borrow the figures from the previous column instead of reporting them. Suppose you need to subtract "867" from "932". First, configure the schedule to read "932" and then proceed with the subtraction starting from the left column.
- "9 - 8 = 1", you must therefore leave only one grain raised in the hundreds column.
- In that of the tens you cannot subtract "6" from "3", so you borrow the number "1" from the hundreds (thus zeroing the column) and proceed by removing "6" from "13" which gives "7" (a lowered bead in the upper sector and two raised beads in the lower one).
- Repeat the same process for the unit column. Borrow a bead from the tens (which becomes "6") and subtract "7" from "12" instead of "2".
- You should get the number "5" in the last column: 932 - 867 = 65.
Part 3 of 4: Multiplication
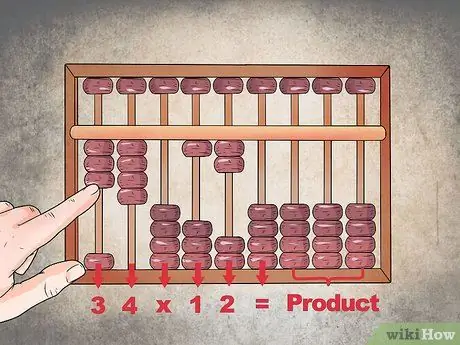
Step 1. Report the problem on the schedule
Start from the far left column. Suppose you need to multiply "34" and "12", then assign each column the value "3", "4", "X", "1", "2" and "=". Leave the remaining columns on the far right free to write down the solution.
- The symbols "X" and "=" are indicated with zero columns.
- The schedule should be configured with three beads at the top in the first column on the left and four in the next followed by a zeroed column ("X"). Afterward, you should have one grain facing up, two grains at the top of the column that follows, and another empty ("="). You need the rest of the abacus to report the product.
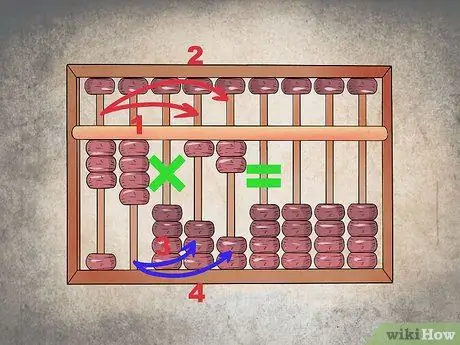
Step 2. Do the multiplication by alternating columns
In this operation it is essential to respect a precise order. You must multiply the first column with the one immediately after the pause ("X") and then always multiply the first column with the second after the "X" sign. Then multiply the second column with the first of the second factor and then again with the second of the second factor.
If you are working with very large numbers, always follow the same pattern: start with the leftmost digit and move gradually to the right

Step 3. Write down the products in the correct order
It starts from the first column assigned to the result, after the zeroed column that corresponds to the "=" sign. You must keep moving the grains to the right portion of the abacus as you multiply the individual digits. To solve the "34 x 12" operation:
- First, multiply "3" with "1" by putting the result in the first column of products; bring three beads to the top in the seventh column.
- Then multiply "3" by "2" and configure the eighth column accordingly; lower one bead from the upper sector and lift one from the lower sector.
- When you multiply "4" with "1", add the product ("4") to the eighth column, the second of the products. Since you have to add "4" to "6", put a bead on the first column of the result, so that this is configured with the number "4" (four grains of the lower section upwards); the eighth column must have the number "0", so all the beads are in the starting position.
- Write the product of the last two digits, "4" and "2", in the last column of the solution; at this point, the product columns should indicate "4", "0" and "8", so the solution is "408".
Part 4 of 4: Division
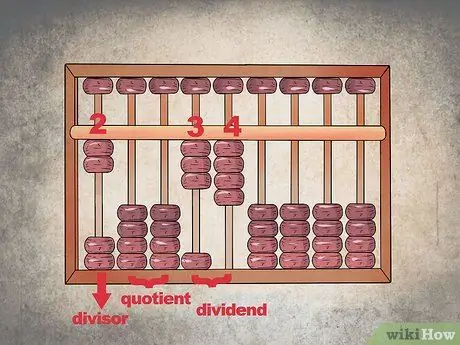
Step 1. Leave empty columns for the solution to the right of the divisor and dividend
When you do this arithmetic operation with the abacus, you have to return the divider to the far left columns, leave a couple of blank spaces and then represent the dividend. The columns that remain on the right are used for calculations and to enter the quotient; for the moment leave them empty.
- For example, to divide "34" by "2", put the number "2" in the leftmost column, leave two blank and then assign the number "34" to the next ones. The rest of the spaces make up the section of the solution.
- To configure the abacus as described, raise two beads in the first column on the left, leave the next two in position "0", raise three beads in the fourth column and four in the fifth; the grains you move all belong to the lower sector.
- The two empty columns between the divider and the dividend serve only as a visual separator to avoid confusion.
Step 2. Write down the quotient
Divide the first digit of the dividend ("3") by the divisor ("2") and put the quotient in the first empty column of the solution; the "2" is in the "3" once, so it returns the number "1".
- To proceed, lift a bead from the lower section of the first column of the solution.
- If you wish, you can leave a blank space between the dividend and the quotient to better distinguish the two sectors as you perform the calculations.
Step 3. Determine the rest
The next step is to multiply the quotient of the first column ("1") by the divisor ("2") and find the remainder; the product ("2") must be subtracted from the dividend of the first column; at this point, you get a new dividend of "14".
To represent the number "14", lower two grains of the lower portion of the fifth column that are currently close to the central bar; in doing so, only one bead remains upwards
Step 4. Repeat the procedure
Write down the second digit of the quotient in the second column of the solution and subtract the product from the dividend (in this case it is zero). Now on the abacus you should read "2" followed by two empty columns and then "1", "7" (which make up the quotient, ie "17").
- In the far left column there should be two grains of the lower sector pushed upwards.
- Then there are several empty columns.
- Then you meet a column with a bead of the lower sector pushed upwards which represents the first digit of the solution.
- In the next column there are two grains of the lower sector close to the central bar and one of the upper sector pushed down.






