How to Learn Algebra (with Pictures)

2024 Author: Samantha Chapman | [email protected]. Last modified: 2024-01-17 17:31

Algebra is important and indispensable for tackling the most advanced mathematics topics during middle and high school. However, some basic concepts can be a bit complex for beginners to understand for the first time. If you have some difficulty with the fundamentals of algebra, don't worry; with a few more explanations, a few simple examples and a few tips, you will be able to improve and solve problems like a math professional.

Steps

Part 1 of 5: Learning the Basic Rules of Algebra

Step 1. Review basic math operations

To start learning algebra, you need to know the four basic operations: addition, subtraction, multiplication and division. Elementary school mathematics is essential for studying algebra. If you do not master this subject, then it will be very difficult to fully understand the more complex concepts that will follow. If you need to review the operations, you can read this article.

You don't have to be a genius at mind operations to solve math problems. In most cases you will be allowed to use a calculator to save time when you need to go through these simple steps. However, you still need to be able to do the four basic math operations without a calculator when this tool is not allowed

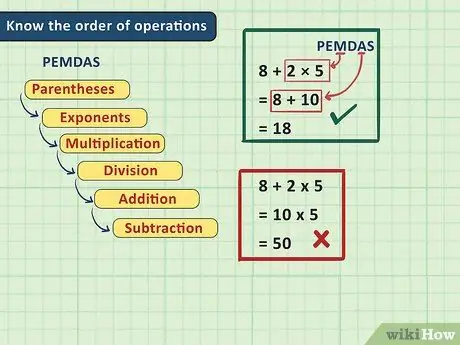
Step 2. Learn the order of operations

For starters, one of the most challenging parts of solving algebraic equations is the starting point. Fortunately, there is a specific order to be respected: first the operations contained in the parentheses are solved, then the powers, multiplications, divisions, additions and finally the subtractions. A mnemonic trick to help you remember this order is the English acronym PEMDAS. You can do some research or reread the math text from previous school years to remember how to follow the order of operations. Here is a brief summary:

• P.arentesi.
• ANDsponking.
• M.oltiplication.
• D.ivision.
• TOdiction.
• S.obtaining.

• This order is very important when studying algebra, because solving a problem by following a wrong process often leads to an incorrect result. For example, if you were to solve the expression 8 + 2 × 5 and first add the 2 with the 8, you would get 10 × 5 = 50, but the correct order of operations requires that first 2 be multiplied by 5 and then 8 is added, obtaining 8 + 10 =

  Step 18.. Only the second answer is the right one.

Step 3. Learn to use negative numbers

They are very common in algebra, so it is worth reviewing how to add, subtract, multiply and divide them before starting to study this branch of mathematics. Here are some topics about negative numbers you should remember and review; you can do some research to recall both how to add and subtract negative numbers, and how to multiply and divide them.

• If you draw the number line, the corresponding negative value of a positive number is exactly the same distance from zero, but in the opposite direction.
• If you add two negative numbers together you get a third value even more negative (in other words you will find a number in absolute value greater, but since it is preceded by the negative sign, it will be even lower).
• Two negative signs cancel each other out, so subtracting a negative number is equivalent to adding a positive number.
• Multiplying or dividing two negative numbers together leads to a positive result.
• Multiplying or dividing a positive number with a negative one leads to a negative result.

Step 4. Learn how to organize long problems

Although simple problems can be solved in no time, complex ones require several steps. To avoid errors, you must maintain a rigorous organization and logic, rewriting the expression every time you perform operations or simplifications, until you get the final answer. If you are facing an equation where the variable appears on both sides of the equality sign, try to keep all the "=" symbols of each step in columns, so that the sheet appears ordered, so you will be less likely to make mistakes.

• Consider, for example, the expression 9/3 - 5 + 3 × 4. You should organize the development of this problem in this way:

  9/3 - 5 + 3 × 4.

  9/3 - 5 + 12.

  3 - 5 + 12.

  3 + 7.

  Step 10..

Part 2 of 5: Understanding Variables

Step 1. Look for all symbols that are not numbers

With the study of algebra, you will begin to notice the presence of letters and symbols in mathematical problems, in addition to numbers. These letters are called variables. However, these are not elements that lead to confusion, as it might seem at first sight; they are simply a way of expressing numbers whose value is unknown. Below is a short list of the most used variables in algebra:

• Letters like x, y, z, a, b, c.
• The letters of the Greek alphabet such as theta that is θ.
• Remember that not all symbols represent unknown variables; for example, pi (π) is approximately 3, 1459.

Step 2. Think of variables as "unknown" numbers

As mentioned above, variables are nothing more than numbers whose value is unknown. In other words, there are numbers that can replace the unknown value and that make the equation true. Your goal in an algebra problem is usually to find the value of these unknowns; imagine it as a "mystery number" that you need to find.

• Evaluate the equation 2x + 3 = 11, where x is the variable. This means that there is a number that substituted for x makes all the expression written to the left of the equal equal to the value of 11. Since 2 × 4 + 3 = 11, then you can say that x =

  Step 4..

• A trick to start understanding the function of unknowns, or variables, is to replace them with a question mark. For example, you can rewrite the equation 2 + 3 + x = 9 as 2 + 3 + ?

  = 9. In this way it is easier to realize what you are looking for: your goal is to find which number added to 2 + 3 = 5 can give you the value 9. The answer, of course, is

  Step 4..

Step 3. If a variable appears more than once in the problem, you can simplify it

How to behave if an unknown is repeated several times within the equation? Although it may seem like a difficult question to answer, know that the only thing you have to do is to consider the variables as a normal number; in other words, you can add them, subtract them and so on with the only constraint that they must be similar. This means that x + x = 2x but x + y is not equal to 2xy.

• Consider the equation 2x + 1x = 9. In this case you can add 2x and 1x together to get 3x = 9. Since 3 x 3 = 9, then you can say that x =

  Step 3..

• Remember that you can only add similar variables together. In the equation 2x + 1y = 9, you cannot proceed to the sum between 2x and 1y, because they are two different variables.
• This is also true when the same variable is repeated twice, but with a different exponent. Suppose you have to solve the equation 2x + 3x² = 10; in this case you cannot add 2x with 3x² because the variable x is expressed with different exponents. Read this article to find out more.

Part 3 of 5: Learning to Solve Equations by "Simplification"

Step 1. Try to isolate the variable in the algebraic equations

Solving an algebraic equation usually means finding the value of the unknown that makes equality true; the equation is presented as a series of operations between numbers and variables written on both sides of the equal sign (=); for example x + 2 = 9 × 4. To find the value of the unknown, you have to isolate it to the right or left of the same (the choice of side does not affect the result).

If we take into account the previous example (x + 2 = 9 × 4), we need to "get rid" of the "+ 2" on the left. To do this, just subtract the number 2, thus remaining with x = 9 × 4. However, to keep the equality true, you must also subtract the number 2 from the right side of the equation and you will therefore have x = 9 × 4 - 2 Following the order of operations, you must first multiply and finally subtract to get x = 36 - 2 = 34.

Step 2. Cancel the addition with a subtraction (and vice versa)

As shown in the previous step, to isolate the x on one side of the equation it is often necessary to eliminate the numbers that are close to it. To obtain this result, the "opposite" operation must be performed on both sides of the equation. Consider, for example, the equation x + 3 = 0. Since there is a "+ 3" next to x, you can add a "- 3" to both terms on either side of the equal sign and you get x = -3.

• In general, addition and subtraction are "reverse" operations, so one allows you to eliminate the other. Here are some examples:

  For addition, the reverse operation is subtraction. For example, x + 9 = 3 → x = 3 - 9.

  For subtraction, the reverse operation is addition. For example, x - 4 = 20 → x = 20 + 4.

Step 3. Eliminate multiplication with division (and vice versa)

Working with these operations is slightly more difficult than adding and subtracting, but the same "opposite" relationship exists between them. If you see "× 3" on one side of the equation, you can eliminate it by dividing both terms by 3 and so on.

• When you work with multiplication and division, you must apply the inverse operation to all the numbers that appear on the other side of the equality sign, regardless of how many there are. Here is an example:

  For multiplication, the reverse operation is division. For example, 6x = 14 + 2 → x = (14 + 2) /6.

  For division, the reverse operation is multiplication. For example, x / 5 = 25 → x = 25 × 5.

Step 4. Delete the exponents by extracting the root (and vice versa)

Powers are a rather advanced pre-algebraic argument; if you still don't know them, you can read this article and get various information. The "inverse" operation of the power is the extraction of the root with an index equal to the exponent of the power itself. For example, the inverse operation of a power with exponent ² is the square root (√), for a power with exponent ³ is the cube root (³√) and so on.

• At first you may feel confused but, in these cases, you just need to extract the root of both terms that appear on the sides of the equality sign to eliminate a power. On the contrary, all you need to do is raise to a power to eliminate the roots. Here are some examples:

  If you need to eliminate the potency, extract the root. For example, x² = 49 → x = √49.

  If you need to remove the roots, raise to a potency. For example, √x = 12 → x = 12².

Part 4 of 5: Hone Your Algebraic Skills

Step 1. Use images to simplify problems

If you have some difficulty visualizing algebraic problems, then try using diagrams or images to illustrate the equation. You can also use a group of physical items (such as bricks or coins) if you have them available.

• Try to solve the equation x + 2 = 3 with the squares method (☐).

  x +2 = 3.

  ☒+☐☐ =☐☐☐.

  At this point you can subtract 2 from both sides of the equality sign by removing two squares (☐☐) and you will get:

  ☒+☐☐-☐☐ =☐☐☐-☐☐.

  ☒ = ☐, that is x =

  Step 1..

• Solve another example, like 2x = 4.

  ☒☒ =☐☐☐☐.

  Now you need to divide both terms by two by separating the squares into two groups:

  ☒|☒ =☐☐|☐☐.

  ☒ = ☐☐ that is x =

  Step 2..

Step 2. Use "common sense", especially when solving descriptive problems

When you need to rewrite a descriptive problem in mathematical terms, try to verify the formula by inserting simple values instead of the unknown. Does the equation make sense for x = 0, for x = 1 or for x = -1? It's easy to make mistakes when writing down p = 6d in place of p = d / 6, but these simple tricks help you do a quick check before continuing with your calculations.

For example, consider the problem that a football field is 30m longer than it is wide. You can represent this data with the equation l = w + 30. You can check if the equality makes sense by inserting some simple value in place of w. Suppose the field is 10m wide, then it means it is 10 + 30 = 40m long. If it were 30m wide, then it would be 30 + 30 = 60m long and so on. All this makes sense, given that the length of the field is greater than its width respecting the assumption of the problem. The equation is therefore reasonable

Step 3. Remember that in algebra the solutions are not always integers

Often the result is formulated with advanced representations that are not consistently simple integers. You will come across decimals, fractions or irrational numbers very frequently. The calculator will be a useful tool for finding these complex solutions, but remember that your teacher may ask you to formulate the answer precisely and not with an infinite series of decimal places.

For example, consider the case where simplifying an equation led you to x = 1250⁷. If you enter 1250⁷ on the calculator, you'll get a number with several digits (plus, since calculator monitors aren't huge, the full solution won't be shown either). In this case it is appropriate to leave the result as 1250⁷ or rewrite it in a simplified way thanks to scientific notation.

Step 4. Once you have become familiar with algebraic concepts, you can also try factoring

One of the most difficult skills to acquire when it comes to algebra is the factoring; however, this allows you to reduce complex equations to simpler forms, so we can consider the decomposition a sort of mathematical shortcut. The decomposition is a semi-advanced algebraic topic, so it is advisable to read the article cited above to review the main concepts and unravel any doubts. Below is a short list of tips for factoring equations:

• The equations expressed with the form ax + ba, can be simplified as a (x + b). For example, 2x + 4 = 2 (x + 2).
• Equations written as ax² + bx can be decomposed as cx ((a / c) x + (b / c)) where c is the greatest common divisor of a and b. For example, 3y² + 12y = 3y (y + 4).
• The equations described as x² + bx + c can be represented as (x + y) (x + z) where y × z = c and yx + zx = bx. For example, x² + 4x + 3 = (x + 3) (x + 1).

Step 5. Practice always and consistently

To improve in algebra (and in all other branches of mathematics) it is essential to do a lot of homework and repeat problems. You don't have to worry, if you pay attention during lessons, do your homework and ask for further help from the teacher or other students when you need it, then algebra will become a subject that you will be able to master perfectly.

Step 6. Ask your teacher to help you understand the more complex topics and passages

If you can't juggle this matter, don't panic! You don't have to learn alone. The professor is the first person you should ask your questions. At the end of the lesson, politely ask him for some help. A good teacher is usually more than happy to explain the day's topics to you once more by making an appointment for you at the end of the lessons and maybe even give you additional study material.

If for some reason your teacher cannot help you, inquire at the institute if a mentoring service is active. Many schools organize some sort of remedial courses in the afternoon that allow you to have other explanations and provide you with all the tools you need to excel with algebra. Remember that using these free supports is not something to be ashamed of, on the contrary it is a sign of intelligence, as you show that you are mature enough to want to solve your problems

Part 5 of 5: Examine More Complex Topics

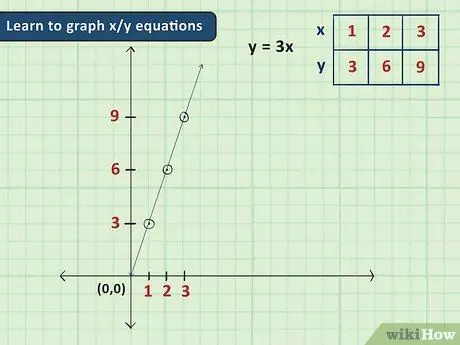
Step 1. Learn the graphical representation of linear equations

Graphs are a very precious tool of algebra, because they allow you to visualize numerical concepts through images that are easy to understand. Usually, at the beginning, the graphical problems are limited to equations with two variables (x and y) and only reference systems are used with the abscissa and ordinate axes. With this type of equation, all you have to do is assign a value to the variable x to get the corresponding value of y (or vice versa), in order to derive a pair of coordinates on the graph.

• Take as an example the equation y = 3x, if you assume x = 2 then y = 6. This means that the point with coordinates (2, 6) (two spaces from the origin to the right and six spaces from the origin to the top) is part of the graph of the equation.
• The equations that respect the form y = mx + b (where m and b are numbers) are quite common in basic algebra. The corresponding graph always has a slope m and crosses the ordinate axis at the point y = b.

Step 2. Learn to solve inequalities

What to do when the algebraic problem does not include the use of the equality sign? Don't worry, the process of getting to the solution isn't that different from usual. For inequalities, which use the symbols> ("greater than") and <("less than"), you have to proceed as usual. You will get a solution which will be greater or less than the variable.

• Consider, for example, the inequality 3> 5x - 2. To solve it, proceed as for a normal equation:

  3> 5x - 2.

  5> 5x.

  1> x o x <1.

• This means that the inequality is true for any value of x less than 1. In other words, it means that x could be 0, -1, -2, and so on. If you replace x with these numbers, you will always get a number lower than 3.

Step 3. Work on quadratic equations

This is also a topic that puts those who approach algebra for the first time in difficulty. Quadratic equations are defined as those that are expressed with the form x² + bx + c = 0, where a, b and c are non-zero numbers. These equations are solved using the formula x = [-b +/- √ (b² - 4ac)] / 2a. Be very careful because the +/- symbol means you have to subtract and add to find two solutions to this type of problem.

• Consider the 3x quadratic equation² + 2x -1 = 0.

  x = [-b +/- √ (b² - 4ac)] / 2a

  x = [-2 +/- √ (2² - 4(3)(-1))]/2(3)

  x = [-2 +/- √ (4 - (-12))] / 6

  x = [-2 +/- √ (16)] / 6

  x = [-2 +/- 4] / 6

  x = - 1 and 1/3

Step 4. Try practicing systems of equations

It may seem impossible to solve multiple equations all at once, but when these are simple, know that it is not that complex. Algebra teachers often use a graphical approach to this kind of problem. When you have to work with a two-equation system, the solutions are represented by the intersection points of the various graphs.

• For example, consider the system that contains these two equations: y = 3x - 2 and y = -x - 6. If you draw the corresponding graphs, you notice that a line is directed upwards with a rather "steep" slope, while the other goes downwards respecting a smaller angle. Since these lines cross at the point with coordinates (-1, -5), this is the solution.

• If you want to check, you can enter the coordinate values in the equations to make sure that the equalities are respected:

  y = 3x - 2.

  -5 = 3(-1) - 2.

  -5 = -3 - 2.

  -5 = -5.

  y = -x - 6.

  -5 = -(-1) - 6.

  -5 = 1 - 6.

  -5 = -5.

• Both equations are "verified", so your answer is correct.

Advice

• There are thousands of websites that help students understand algebra. For example, just type the words "help in algebra" into your favorite search engine and you will get dozens of pages as a result. You can also visit the Math section of wikiHow, you will find a lot of information, so start your search!
• On the web you can find many sites dedicated to mathematics and algebra; in some cases you can also have access to online universities and tutorials with videos. You can do a short search on YouTube, with your search engine, and start using some support tools. Also do not underestimate the help that your own school can offer you, such as support courses, afternoon lessons and exercises and so on.
• Remember that the best way to learn algebra is to rely on people who know it deeply and who make you feel at ease. Talk to your friends or classmates, organize a study group if you need help.