A matrix is a rectangular arrangement of numbers, symbols or expressions in rows and columns. To multiply the matrices, it is necessary to multiply the elements (or numbers) in the row of the first matrix by the elements of the columns of the second table and add their products. You can multiply matrices in a few simple steps that require addition, multiplication and correct placement of the results. Here's how to do it.
Steps
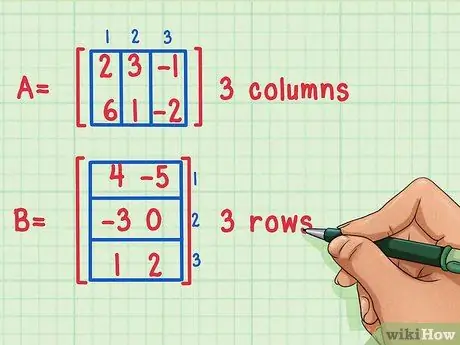
Step 1. Make sure the matrices can be multiplied
It is possible to multiply two matrices together only if the number of columns of the first matrix is equal to the number of rows of the second.
These matrices can be multiplied because the first matrix, A, has 3 columns, while the second matrix, B, has 3 rows
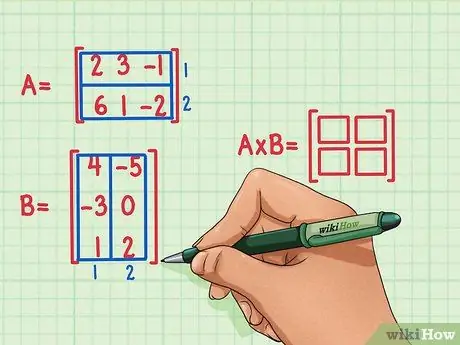
Step 2. Mark the dimensions of the product matrix
Creates a new blank matrix of the product dimensions of the two matrices. The matrix representing the product of matrices A and B will have the same number of rows as the first and the same number of columns as the second. Blank boxes can be drawn to indicate the number of rows and columns in this matrix.
- Matrix A has 2 rows, so the product will have 2 rows.
- Matrix B has 2 columns, so the product will have 2 columns.
- The product matrix will have 2 rows and 2 columns.
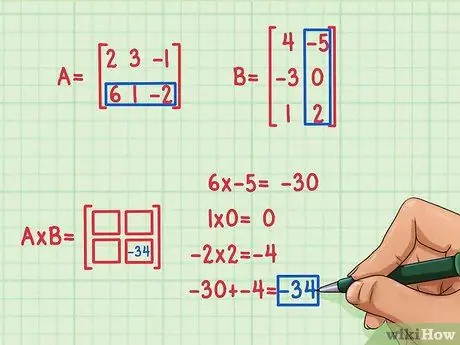
Step 3. Find the dot product
To find it, you need to multiply the first element in the first row with the first element of the first column of the second matrix, the second element of the first row of A with the second element of the first column of B, and the third element of the first row of A with the third element of the first column of B. Then add their products to find the missing element to insert in the square of place 1, 1, first row and first column. Suppose you have decided to find the element of place 2, 2 (bottom right) in the product matrix. Here's how it's done:
- 6 x -5 = -30
- 1 x 0 = 0
- -2 x 2 = -4
- -30 + 0 + (-4) = -34
-
The dot product is -34 and fits in the lower right of the product matrix.
When multiplying matrices, the dot product will go to position R, C, indicating with R the row number of the first matrix and with C the column number of the second matrix. For example, when you found the dot product of the second row of matrix A for the second column of table B, the answer, -34, went into the bottom row and right column of the matrix product in place 2, 2
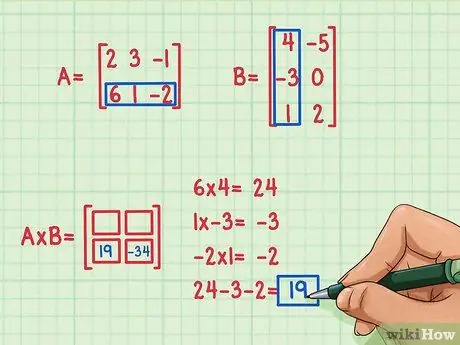
Step 4. Find the second dot product
Suppose we want to find the term at the bottom left of the product matrix, in place 2, 1. To find this term, you simply multiply the elements of the second row of A by the elements of the first column of B and then add. Use the same method used to multiply the first row of A with the first column of B: find the dot product again!
- 6 x 4 = 24
- 1 x (-3) = -3
- (-2) x 1 = -2
- 24 + (-3) + (-2) = 19
- The dot product is 19 and goes in the lower left place.
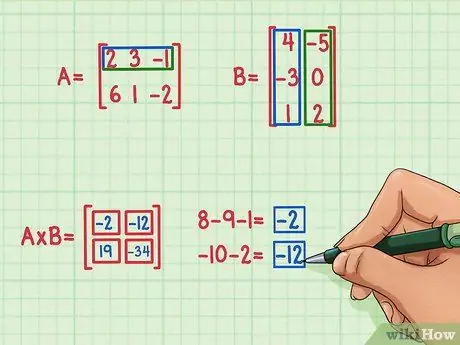
Step 5. Find the remaining two dot products
To find the upper left term of the product matrix, find the dot product of the row of matrix A and the first column of matrix B. Here's how:
- 2 x 4 = 8
- 3 x (-3) = -9
- (-1) x 1 = -1
- 8 + (-9) + (-1) = -2
-
The dot product is -2 and goes top left.
To find the term on the top right of the product matrix, just find the dot product of the top row of matrix A by the right column of matrix B. Here's how to do it:
- 2 x (-5) = -10
- 3 x 0 = 0
- (-1) x 2 = -2
- -10 + 0 + (-2) = -12
- The dot product is -12 and goes to the top right.
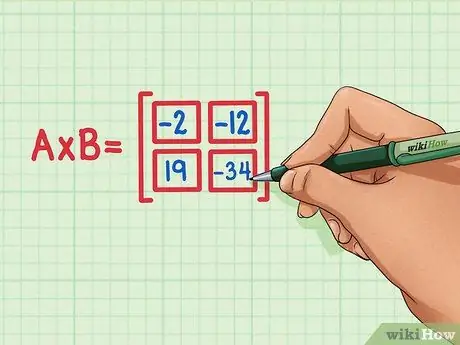
Step 6. Check that all four dot products are in the correct position of the matrix product
19 should be bottom left, -34 should be bottom right, -2 should be top left, and -12 should be top right.
Advice
- If the stroke representing a row needs to be extended to cross a column, go ahead without fear! This is just a visualization technique to make it easier to understand which row and which column should be used to process each item of the product.
- Write down the sums. Multiplication of matrices involves a lot of calculations and it is very easy to get distracted and lose track of which numbers you are multiplying.
- The product of two matrices must have the same number of rows as the first matrix and the same number of columns as the second.






