For those who don't know how to use it, the slide rule looks like a ruler designed by Picasso. There are at least three different scales, and most of them do not indicate values in an absolute sense. But after you learn about this tool, you will understand why it proved so useful over the centuries, before the advent of pocket calculators. Line up the numbers on the scale and you can multiply any two factors, with a less complicated process than with pen and paper.
Steps
Part 1 of 4: Understanding the Slide Rules
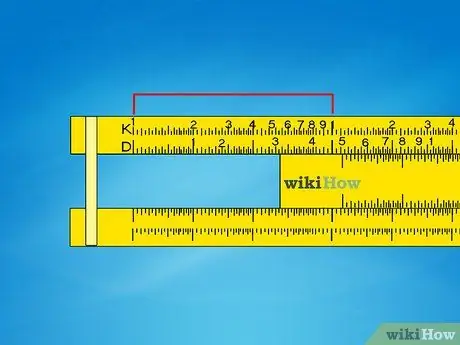
Step 1. Note the interval between the numbers
Unlike a normal line, the numbers are not equidistant on the slide rule; on the contrary, they are spaced using a particular logarithmic formula, denser on one side than on the other. This allows you to align the scales to obtain the result of mathematical operations, as described below.
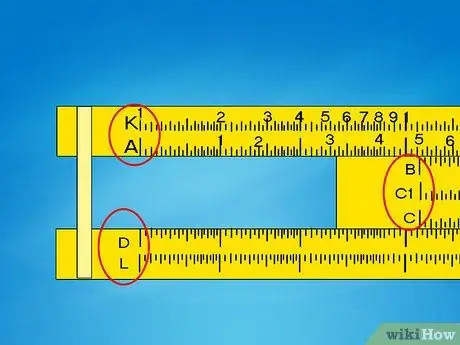
Step 2. Look for the names of the stairs
Each scale should have a letter or symbol on the left or right. This guide assumes that your slide rule uses the most common scales:
- The C and D scales have the appearance of a single linear line, reading from left to right. These are called "single decade" scales.
- The A and B scales are “double decade” scales. Each has two smaller lines aligned.
- The K scale is a triple ten, that is, with three aligned lines. It is not present in all models.
- The C | stairs and D | they are the same as C and D, but read from right to left. These are usually red in color, but they are not present in all models.
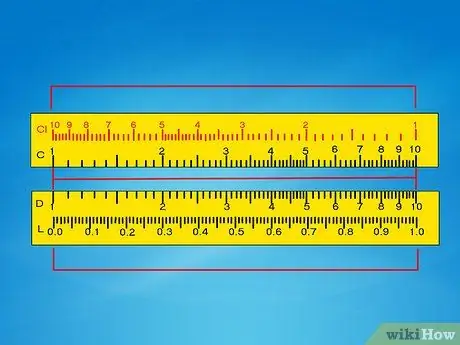
Step 3. Try to understand the divisions of the scale
Take a look at the vertical lines of the C or D scale, and get used to reading them:
- The primary numbers on the scale start from 1 on the left end, continue up to 9, and end with another 1 on the right end. They are usually all marked.
- The secondary divisions, marked by the vertical lines in second place in order of height, divide each primary number by 0, 1. Don't get confused if they are called “1, 2, 3”; remember that they actually represent “1, 1; 1, 2; 1, 3 "and so on.
- There are usually smaller divisions, which represent increments of 0.02. Pay close attention, as they may disappear at the end of the scale, where the numbers approach each other.
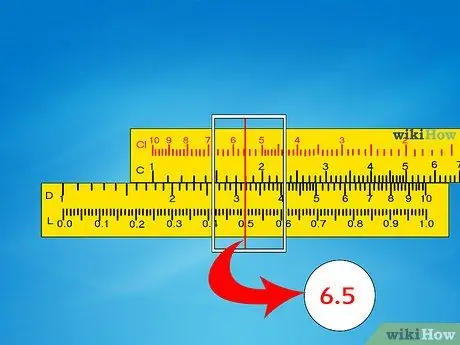
Step 4. Don't expect accurate results
Often you will have to make the "best guess" when reading a scale where the result is not exactly on one line. Slide rules are used for quick calculations, not for purposes that require extreme precision.
For example, if the result is between 6, 51 and 6, 52, write the closest value. If you don't know it, write 6, 515
Part 2 of 4: Multiplying the Numbers

Step 1. Write the numbers you want to multiply
- In example 1 of this section we will calculate 260 x 0, 3.
- In example 2 we will calculate 410 x 9. The second example is more complicated than the first, so you should do this first.

Step 2. Shift the decimal points for each number
The slide rule only includes numbers between 1 and 10. Move the decimal point in each number you multiply, so that it is between these values. After the operation is completed, we will move the decimal point to the right place, as will be described at the end of this section.
- Example 1: To calculate 260 x 0, 3, start at 2, 6 x 3.
- Example 2: To calculate 410 x 9, start at 4, 1 x 9.

Step 3. Find the smallest number on the D scale, then slide the C scale onto it
Find the smallest number on the D scale. Slide the C scale so that the number 1 on the far left (called the left index) is aligned with that number.
- Example 1: slide the C scale so that the left index is in line with 2, 6 on the D scale.
- Example 2: slide the C scale so that the left index is aligned with 4, 1 on the D scale.
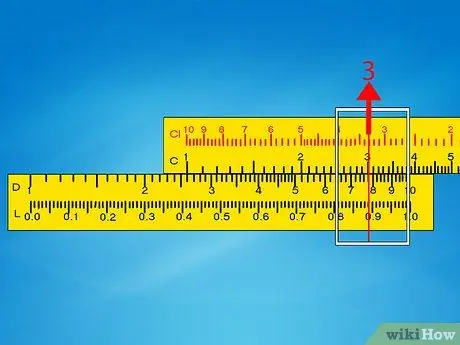
Step 4. Slide the cursor to the second number on the C scale
The cursor is the metal object that slides along the entire line. Line it up with the second factor of your multiplication on the C scale. The cursor will indicate the result on the D scale. If it can't slide that far, go to the next step.
- Example 1: slide the cursor to indicate 3 on the C scale. In this position it should also indicate 7, 8 on the D scale. Go directly to the approximation step.
- Example 2: Try to slide the cursor to point to 9 on the C scale. For most slide rules this will not be possible, or the cursor will point to the void outside of the D scale. Read the next step to understand how to solve this problem.
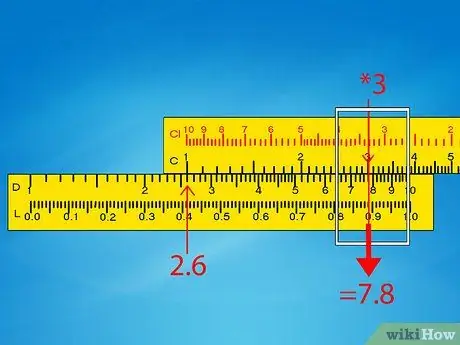
Step 5. If the cursor does not scroll to the result, use the right index
If it is blocked by a detent in the center of the slide rule, or if the result is off the scale, take a slightly different approach. Slide the C scale so that the right index or the 1 on the far right is positioned on the greater factor of the multiplication. Slide the cursor to the position of the other factor on the C scale and read the result on the D scale.
Example 2: Slide the C scale so that the 1 on the far right is aligned with the 9 on the D scale. Slide the cursor over 4, 1 on the C scale. The cursor indicates between 3, 68 and 3, 7 on the scale D, so the result should be approximately 3.69
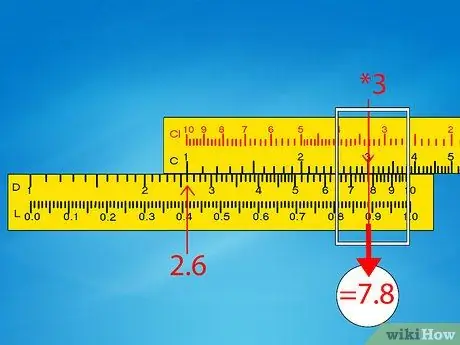
Step 6. Use the approximation to find the correct decimal point
Regardless of the multiplication you perform, the result will always be read on the D scale, which only shows numbers from 1 to 10. You will need to use approximation and mental calculation to determine where to put the decimal point in your real result.
- Example 1: Our original problem was 260 x 0, 3 and the slide rule returned us a result of 7, 8. Round off the original result and solve the operation in your mind: 250 x 0, 5 = 125. It is closer to 78 instead of 780 or 7, 8, so the answer is 78.
- Example 2: Our original problem was 410 x 9 and we read 3.69 on the slide rule. Consider the original problem as 400 x 10 = 4000. The closest result we can get by moving the decimal point is 3690, so this will have to be the answer.
Part 3 of 4: Calculating the Squares and Cubes
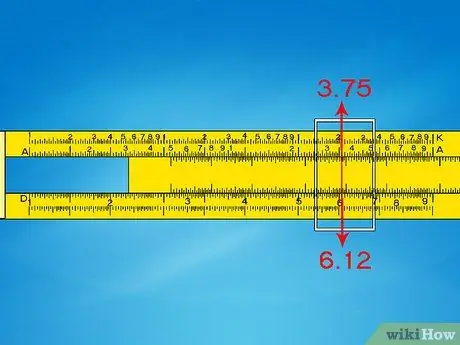
Step 1. Use the D and A scales to calculate the squares
These two scales are usually fixed at one point. Simply slide the metal cursor over the D scale value and the A value will be the square. Just like a math operation, you will have to determine the position of the decimal point by yourself.
- For example, to solve 6, 12, slide the cursor to 6, 1 on the D scale. The corresponding A value is approximately 3.75.
- Approximate 6, 12 a 6 x 6 = 36. Place the decimal point to get a result close to this value: 37, 5.
- Note that the correct answer is 37, 21. The slide rule result is 1% less accurate than in real life situations.
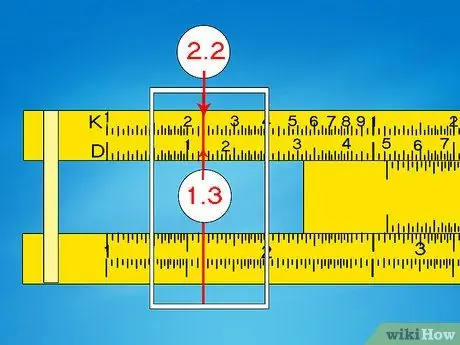
Step 2. Use the D and K scales to calculate the cubes
You just saw how the A scale, which is a half-scale reduced D scale, allows you to find the squares of the numbers. Similarly the K scale, which is a D scale reduced to one third, allows you to calculate cubes. Simply slide the cursor to a D value and read the result on the K scale. Use the approximation to place the decimal.
For example, to calculate 1303, slide the cursor towards 1, 3 on the D value. The corresponding K value is 2, 2. Since 1003 = 1 x 106, and 2003 = 8 x 106, we know the result must be between them. It must be 2, 2 x 106, or 2.200.000.
Part 4 of 4: Calculating the Square and Cubic Roots

Step 1. Convert the number to scientific notation before calculating a square root
As always, the slide rule only understands values from 1 to 10, so you'll need to write the number in scientific notation before finding its square root.
- Example 3: To find √ (390), write it as √ (3, 9 x 102).
- Example 4: To find √ (7100), write it as √ (7, 1 x 103).
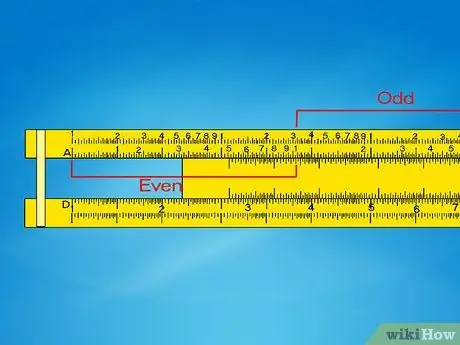
Step 2. Identify which side of the ladder A to use
To find the square root of a number, the first step is to slide the cursor over that number on the A scale. However, since the A scale is printed twice, you will need to decide which one to use first. To do this, follow these rules:
- If the exponent in your scientific notation is even (such as 2 in example 3), use the left side of the scale A (the first decade).
- If the exponent in the scientific notation is odd (such as 3 in example 4), use the right side of the A scale (the second decade).
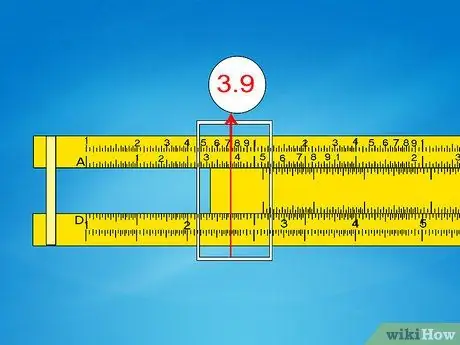
Step 3. Slide the cursor on the A scale
Ignoring exponent 10 for the moment, slide the cursor along the A scale towards the number you finished with.
- Example 3: to find √ (3, 9 x 102), slide the cursor to 3, 9 on the left scale A (you must use the left scale, because the exponent is even, as described above).
- Example 4: to find √ (7, 1 x 103), slide the cursor to 7, 1 on the right scale A (you have to use the right scale because the exponent is odd).
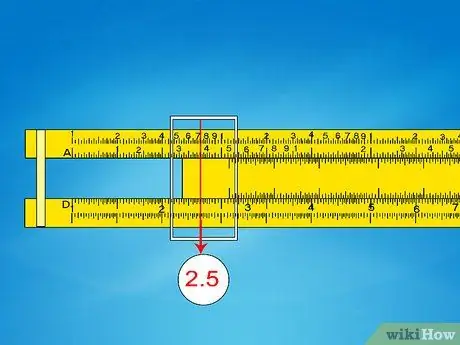
Step 4. Determine the result from the D scale
Read the D value indicated by the cursor. Add "x10 "to this value. To calculate n, take the original power of 10, round down to the nearest even number, and divide by 2.
- Example 3: the D value corresponding to A = 3, 9 is approximately 1, 975. The original number in scientific notation was 102; 2 is already even, so divide by 2 to get 1. The final result is 1.975 x 101 = 19, 75.
- Example 4: the D value corresponding to A = 7, 1 is approximately 8.45. The original number in scientific notation was 103, then round 3 to the nearest even number, 2, then divide by 2 to get 1. The final result is 8.45 x 101 = 84, 5
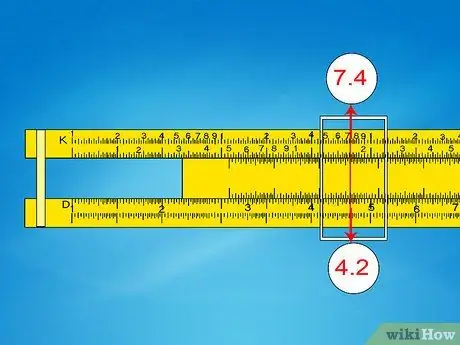
Step 5. Use a similar procedure on the K scale to find the cube roots
The most important step is to identify which of the K scales to use. To do this divide the number of digits in your number by 3 and find the remainder. If the remainder is 1, use the first scale. If it's 2, use the second scale. If it is 3, use the third scale (another way to do this is to repeatedly count from the first to the third scale, until you reach the number of digits in your result).
- Example 5: To find the cube root of 74,000, first count the number of digits (5), divide by 3 and find the remainder (1 remainder 2). Since the remainder is 2, use the second scale. (Alternatively, count the scales five times: 1-2-3-1-2).
- Slide the cursor towards 7, 4 on the second K scale. The corresponding D value is approximately 4, 2.
- Since 103 is less than 74,000, but 1003 is greater than 74,000, the result must be between 10 and 100. Move the decimal point to get 42.
Advice
- There are other functions you can calculate with the slide rule, especially if it includes logarithmic scales, trigonometric scales, or other special scales. Try it out on your own or do some research online.
- You can use multiplication to convert between two units of measurement. For example, since one inch equals 2.54 cm, to convert 5 inches to centimeters simply multiply 5 x 2.54.
- The accuracy of a slide rule depends on the number of divisions on the scales. The longer it is, the more accurate it is.






