3 Ways to Decompose Numbers

Table of contents:

3 Ways to Decompose Numbers
3 Ways to Decompose Numbers
Anonim

Practicing breaking down numbers allows students to understand the general patterns and relationships between the digits of large numbers and the numbers in an equation. You can decompose numbers into hundreds, tens and units or break them down into addends.

Steps

Method 1 of 3: Decompose into Hundreds, Tens and Units

Decomposed Numbers Step 1
Decomposed Numbers Step 1

Step 1. Learn the difference between "tens" and "units

In a two-digit number without the comma (or decimal point), the two digits represent“tens”and“units.”The“tens”are on the left, while the“units”are on the right.

  • The number representing the "units" can be read exactly as it appears. The only numbers that make up the "units" are the numbers 0 to 9 (zero, one, two, three, four, five, six, seven, eight and nine).
  • The number that represents the "tens" has the same aspect as the number that makes up the units. However, when displayed separately, this number is actually followed by a 0, which makes it greater than a number in “units”. Numbers belonging to the "tens" include: 10, 20, 30, 40, 50, 60, 70, 80 and 90 (ten, twenty, thirty, forty, fifty, sixty, seventy, eighty and ninety).
Decomposed Numbers Step 2
Decomposed Numbers Step 2

Step 2. Break down a two-digit number

When you have a two-digit number, it is made up of "units" and "tens". To break down such a number, you will need to divide it into its component parts.

  • Example: Break down the number 82.

    • The 8 represents the "tens", so this part of the number can be separated and rewritten as 80.
    • The 2 represents "units", so this part of the number can be separated and rewritten as 2.
    • In the answer, you will have to write: 82 = 80 + 2

  • Note also that the number written in the usual way is expressed in "standard form", while a decomposed number is written in "extended form".

    In the above example, "82" is the standard form, while "80 + 2" is the extended form

Decomposed Numbers Step 3
Decomposed Numbers Step 3

Step 3. Enter the "hundreds"

When a number is made up of three digits without a comma (or decimal point), it is made up of "units", "tens" and "hundreds". The "hundreds" are those to the left of the number. The "tens" are in the center, while the "units" are on the right.

  • The "units" and "tens" work exactly the same as in two-digit numbers.
  • The number indicating "hundreds" looks the same as the number indicating "units" but, when displayed separately, it is actually followed by two zeros. The numbers that belong to the "hundreds" are: 100, 200, 300, 400, 500, 600, 700, 800, and 900 (one hundred, two hundred, three hundred, four hundred, five hundred, six hundred, seven hundred, eight hundred and nine hundred).
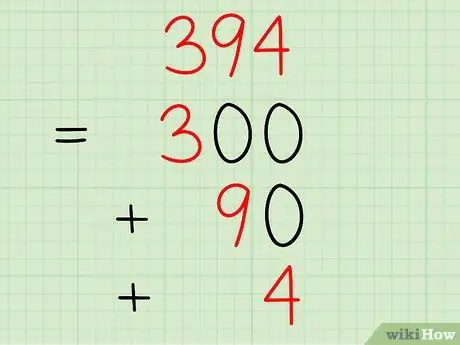
Decomposed Numbers Step 4
Decomposed Numbers Step 4

Step 4. Break down a three-digit number

When you have a three-digit number, it is made up of "units", "tens" and "hundreds". To decompose a number of this type, you will have to divide it into the three parts that make it up

  • Example: Break down the number 394.

    • The 3 represents the "hundreds", so this part of the number can be separated and rewritten as 300.
    • The 9 represents the "tens", so this part of the number can be separated and rewritten as 90.
    • The 4 represents "units", so this part of the number can be separated and rewritten as 4.
    • The final answer will be: 394 = 300 + 90 + 4
    • When you write 394, the number is in standard form. When you write 300 + 90 + 4, the number is in extended form.
    Decomposed Numbers Step 5
    Decomposed Numbers Step 5

    Step 5. Apply this pattern to higher and higher numbers

    You can break down the higher numbers using the same principle.

    • A digit placed in any position can be broken down into a separate part by replacing the numbers to its right with zeros. This is always valid, regardless of how many digits the number has.
    • Example: 5,394,128 = 5,000,000 + 300,000 + 90,000 + 4,000 + 100 + 20 + 8
    Decomposed Numbers Step 6
    Decomposed Numbers Step 6

    Step 6. Learn how decimals work

    You can decompose decimal numbers, but any number after the decimal point must be broken down into a portion of the number also written as a decimal.

    • “Tenths” are used when there is only one digit after the comma or decimal point (or to the right of them).
    • The "cents" are used when there are two digits after the comma (or the decimal point).
    • The "thousandths" are used when there are three digits after the comma (or the decimal point).
    Decomposed Numbers Step 7
    Decomposed Numbers Step 7

    Step 7. Break down a decimal number

    When you have a number with digits both to the left and to the right of the decimal point, you have to break it down by considering both sides.

    • Note that all numbers to the left of the comma can be broken down in the same way as if the comma were not present.

    • Example: Break down the number 431, 58

      • The 4 represents the "hundreds", so this part of the number can be separated and rewritten as 400
      • The 3 represents the "tens", so this part of the number can be separated and rewritten as 30
      • The 1 represents "units", so this part of the number can be separated and rewritten as 1
      • The 5 represents the "tenths", so this part of the number can be separated and rewritten as 0, 5
      • The 8 represents "cents", so this part of the number can be separated and rewritten as 0.08
      • The final answer will be: 431, 58 = 400 + 30 + 1 + 0, 5 + 0, 08

      Method 2 of 3: Decompose into Addends

      Decomposed Numbers Step 8
      Decomposed Numbers Step 8

      Step 1. Understand the concept

      When you break down a number into its addends, you divide it into several sets of other numbers (the addends, in fact) which can be added together to get the original value.

      • When we subtract one addend from the original number, we get the second addend.
      • By adding the addends, the total obtained will be the original number.
      Decomposed Numbers Step 9
      Decomposed Numbers Step 9

      Step 2. Practice with numbers with few digits

      This exercise is very easy when you have single digit numbers (numbers that have only "units").

      You can combine these principles with those learned in the section "Decomposing into Hundreds, Tens and Units" to decompose the higher numbers, but as there are so many addend compositions for the higher numbers, this method will be impossible to use alone with such numbers

      Decomposed Numbers Step 10
      Decomposed Numbers Step 10

      Step 3. Find all the different combinations of addends

      To decompose a number into addends you will have to write down all the possible ways in which you can get the original number add numbers smaller than it.

      • Example: Break the number 7 into its different addends.

        • 7 = 0 + 7
        • 7 = 1 + 6
        • 7 = 2 + 5
        • 7 = 3 + 4
        • 7 = 4 + 3
        • 7 = 5 + 2
        • 7 = 6 + 1
        • 7 = 7 + 0
        Decomposed Numbers Step 11
        Decomposed Numbers Step 11

        Step 4. Use visual aids if needed

        For those trying to learn this concept for the first time, it can be helpful to use visual aids to demonstrate the process in a practical way.

        • Start with a number of items. For example, if the number is seven, start with seven candies.

          • Separate them into two groups by setting one aside. Count the remaining ones and explain that the initial seven candies have been broken down into "one" and "six."
          • Continue to separate the candies into two groups by removing them one at a time from the first and moving them to the second. Count the candies in both groups on each move.
        • You can use a variety of materials, including candy, paper squares, colored pins, blocks or buttons.

        Method 3 of 3: Decomposing to Solve Equations

        Decomposed Numbers Step 12
        Decomposed Numbers Step 12

        Step 1. Let's look at a simple equation consisting of an addition

        You can combine both decomposition methods to rewrite these types of equations in different forms.

        This is easier when applied to simple addition equations, but becomes less practical when applied to longer equations

        Decomposed Numbers Step 13
        Decomposed Numbers Step 13

        Step 2. Break down the numbers in the equation

        Look at the equation and break the numbers into "tens" and "units". If necessary, you can further break down the "units" into smaller numbers.

        • Example: Break down and solve the equation: 31 + 84

          • You can decompose 31 into: 30 + 1
          • You can decompose 84 into: 80 + 4
          Decomposed Numbers Step 14
          Decomposed Numbers Step 14

          Step 3. Rewrite the equation in a simpler form

          The equation can be rewritten so that each part you have broken it into is isolated, or you can combine some of the broken down parts to make it more understandable.

          Example: 31 + 84 = 30 + 1 + 80 + 4 = 30 + 80 + 5 = 100 + 10 + 5

          Decomposed Numbers Step 15
          Decomposed Numbers Step 15

          Step 4. Solve the equation

          After rewriting the equation to a simpler and more understandable form, all you have to do is add the numbers and calculate the total.

Recommended:

3 Ways to Write Numbers in Spanish

3 Ways to Write Numbers in Spanish

Generally speaking, writing numbers in Spanish is not that different from Italian. Roman numerals are also used in this language, but there are obviously some peculiarities of Spanish, especially as regards the higher figures or the use of numeral adjectives.

3 Ways to Memorize Numbers

3 Ways to Memorize Numbers

An ordinary person can usually remember a series of about seven digits through working memory at any given time. Using the techniques described in this article, however, you can memorize many, many more. The key is to use mnemonic methods, which means building associations that are easier to remember than a random series of numbers.

4 Ways to Quickly Add 5 Consecutive Numbers

4 Ways to Quickly Add 5 Consecutive Numbers

Bet with your friends that you are the fastest to add up five consecutive numbers. Use it as a fun joke with friends or (if you go to school) do it to amaze your teacher! Steps Method 1 of 4: Using the number in the center Step 1.

3 Ways to Read Roman Numbers

3 Ways to Read Roman Numbers

Reading the number MMDCCLXVII would not have been a problem for an inhabitant of ancient Rome or for many people of the Middle Ages in Europe who continued to use the Roman numeral system. Learn to read these numbers by following some basic rules.

3 Ways to Decompose a Trinomial

3 Ways to Decompose a Trinomial

A trinomial is an algebraic expression consisting of three terms. Most likely, you will begin to learn how to decompose quadratic trinomials, that is, written in the form x 2 + bx + c. There are several tricks to learn that apply to different types of quadratic trinomials, but you will get better and faster just with practice.