Addition is one of the few things we learn in school that is really required of us in everyday life. Fortunately it is easy to learn; some rules are required, depending on the kinds of numbers to add, but wikiHow has it all under control. Just start from the first point!
Steps
Method 1 of 5: Adding Small Digits

Step 1. Familiarize yourself with the concept of "sum"
Grab a handful of beans (or other small items). Set aside one bean at a time, in a small pile, and count one at a time (1, 2, 3, etc.). Stop when you have some beans in the pile. How many have you taken? Write the number. Now, do the same thing with another pile. Now mix the two piles. How many do you have now? You can count the beans, one at a time, and find out! This is adding up!
For example, your first pile might have 5 beans. Then the second could have 3. When you mix them and count all the beans, you find that you now have 8 beans! Because 5 + 3 is 8
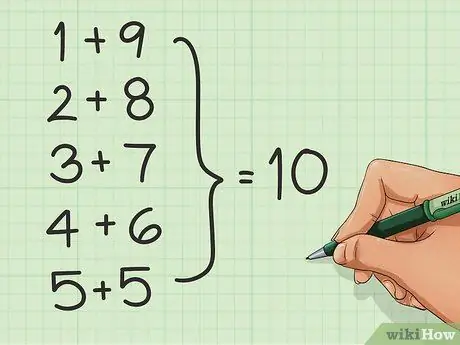
Step 2. Learn the pairs of numbers
Since many base the count on groups of 10 and numbers divisible by 10, you can facilitate addition by learning the pairs of numbers that add up to 10. For example: 1 + 9, 2 + 8, 3 + 7, 4 + 6 and 5 + 5.
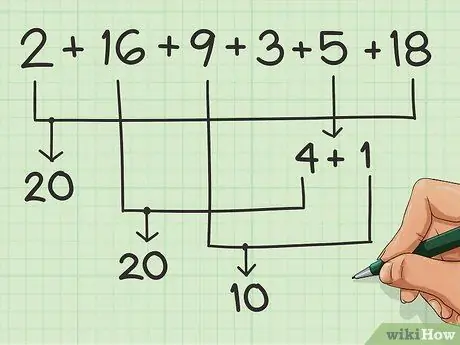
Step 3. Match as many numbers as you can
Match them as many as possible, to make groups of 10.
Let's say you're adding up this series of numbers: 2, 16, 9, 3, 5, 18. You can pair 2 with 18 to get 20. 4 easily goes with 6, so take 4 from 5 and add it to 16 to get a another 20. Then you have a 1 left over from the 5, which you can add to the 9 to get 10
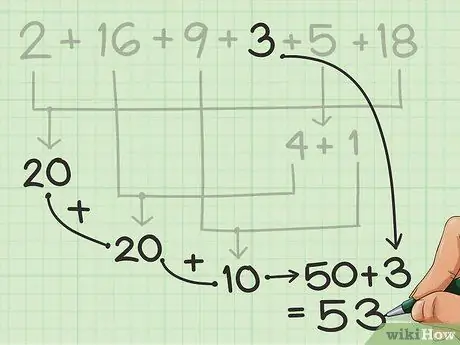
Step 4. Add the leftovers
Count the remaining numbers by hand or by mind, starting with the groups of 10 you have drawn.
In the example from the previous step, you only have 3 left, after getting 50 from the other numbers. It's pretty easy to add up in mind

Step 5. Check the result with your hands
When you can, it is always good to check the calculations using your fingers or other similar methods.
Method 2 of 5: Adding Large Numbers
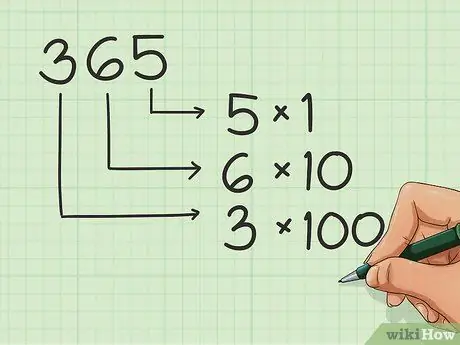
Step 1. Learn the placements of the numbers
When you write numbers, each point in the sequence has a name or gender. Learn these positions to order numbers correctly in addition. For instance:
- A 2 alone is in "units".
- In 20, the 2 is in the "tens".
- In 200, the 2 is in the "hundreds".
- So, in 365, the 5 is in the units, the 6 in the tens, and the 3 in the hundreds.
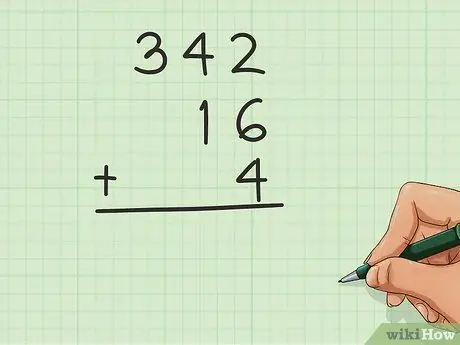
Step 2. Line up the digits
Align them so that each integer to be added is on top of the other. The "positions" are what you will use to line up the numbers, so that all the units overlap. Leave a space on the left when you have a smaller number than the others. For example, adding 16, 4 and 342, you should write like this:
- 342
- _16
- _4
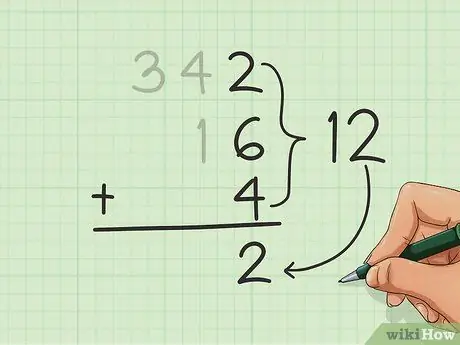
Step 3. Add the first column
Start with the rightmost column and add the numbers together. Once you have the sum (the result of the addition), write the number in the units under all the numbers you are adding, at the bottom of the units column.
In the example above, we get 12 by adding 2, 6, and 4. Write the 2 of the 12 at the bottom of the far right column
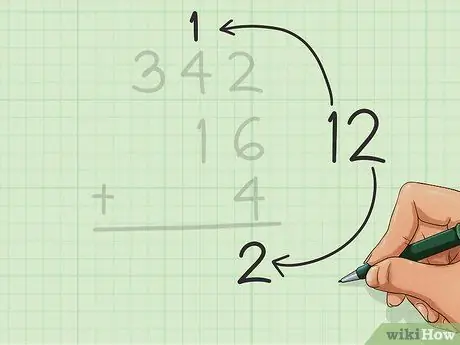
Step 4. Return the tens
If you have a number in the tens, write it at the top of the next column (left).
We have a number in the tens in this example, so we put the 1 of 12 at the top of the center column, above the 4 of 342
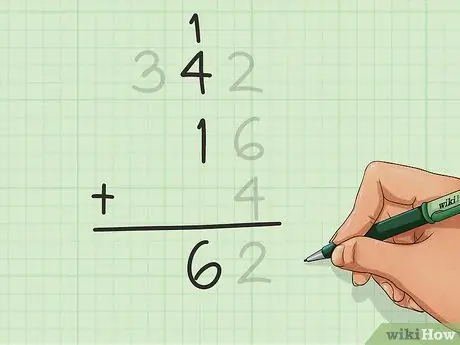
Step 5. Count the next column
Go to the column on the left and count all the digits in this column, including the one you may have added in the previous step. Write the result at the bottom of the column, including any digits in the tens as before.
In this example, we count 1 of 12, plus 4 of 342 and 1 of 16. We get 6
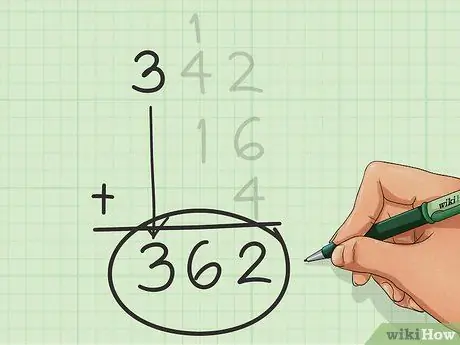
Step 6. Find the final sum
Repeat these counts, moving from right to left, column by column, until you run out of columns. The number you get when you are done is the sum you were looking for.
In this example, the sum is 362
Method 3 of 5: Add with Decimals
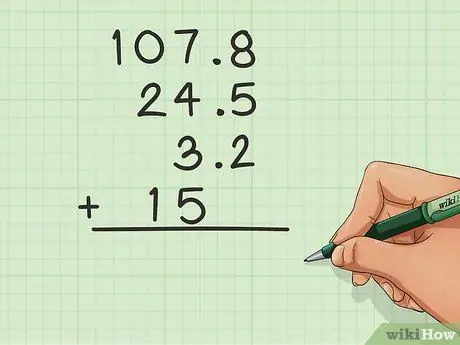
Step 1. Align the decimals
When you have a decimal in a number (for example: 24, 5), you need to be a little more careful with the columns. The main trick is to line up all the numbers using the decimal. The decimals must be in their column. For instance:
- 107, 8
- _24, 5
- _3, 2
- _15, 0
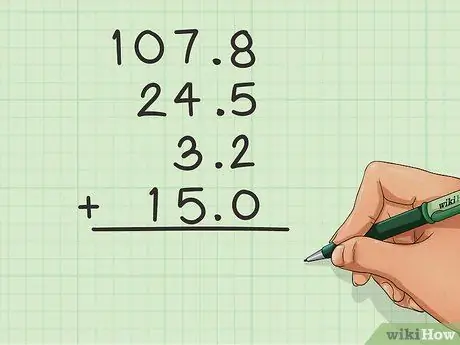
Step 2. Add a decimal if there isn't one
If a number has no digits after the decimal point, add one and put a 0 on the right to help keep the columns in order.
In the example above, the 15 did not have the 0 after the decimal point, so it was added to make the process easier
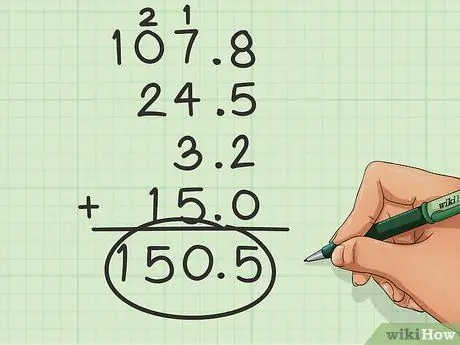
Step 3. Add normally
Once the numbers are lined up, you just need to add them up as you normally would.
The sum of this example will be 150.5
Method 4 of 5: Adding Fractions
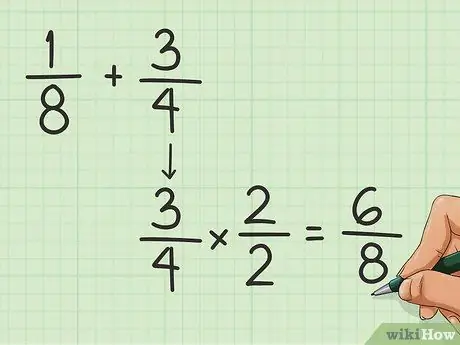
Step 1. Find the common denominator
The denominator is the number below the fraction line. You have to find the common one to add fractions to each other. It can be done by multiplying (or dividing) the upper and lower number of one of the fractions, until the denominator is equal to that of the other fraction. For example, let's say we want to add 1/8 and 3/4:
- You have to make the 4 and the 8 equal. How do you turn a 4 into an 8? Multiply by 2!
- Multiply the 3 and 4 in the 3/4 fraction by 2. You get 6/8.
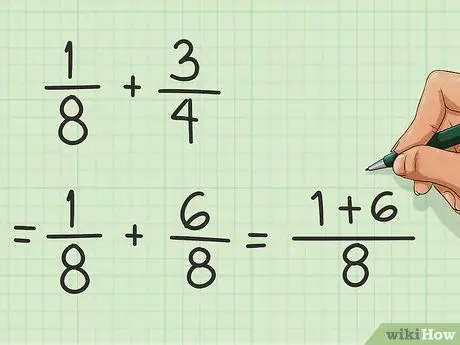
Step 2. Add the numerator
The numerator is the number above the fraction line. Now that you have 1/8 and 6/8, add the 1 and 6 to get 7.
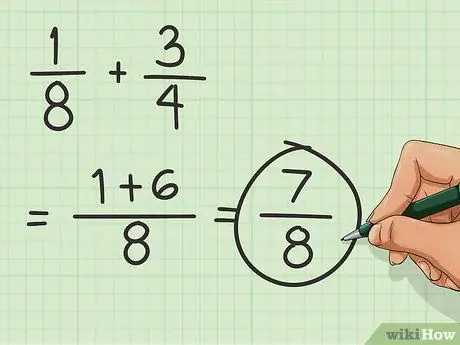
Step 3. Find the sum
Take the added numerators and put them above the denominator. The denominator remains the same. It means that the result of the fraction is 7/8.
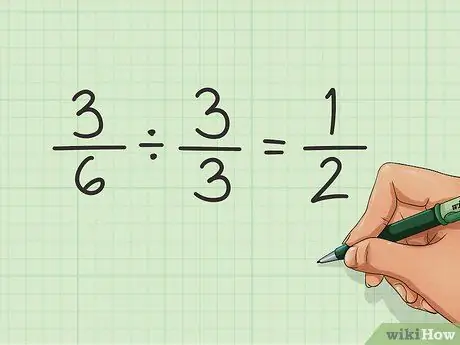
Step 4. Simplify the fraction
You may want to simplify the fraction, using the smallest possible numbers above and below, while still leaving the same overall value. In this example, there is no need to simplify. It is as small as it can be. But if you had a fraction like 3/6, you might want to simplify it.
This can be done by finding the smallest number by which both the numerator and denominator are divisible. In this case it's 3. Divide each number by 3 and you get the reduced fraction, in this case 1/2
Method 5 of 5: Tricks for Adding
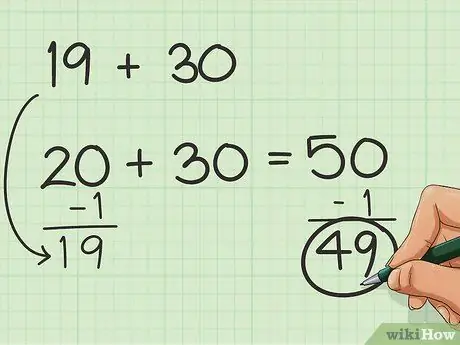
Step 1. Try to balance with simpler numbers
If you only have a couple of numbers to consider, but the numbers don't fit into groups of 10, you can add or subtract numbers to make adding up easier in mind. For example, let's say you need to add 19 + 30. It would be much easier to add 20 + 30, right? So add 1 to 19! You just have to remember to subtract the added number later to get the final result. So: 19 + 1 + 30 = 50 and 50-1 = 49.
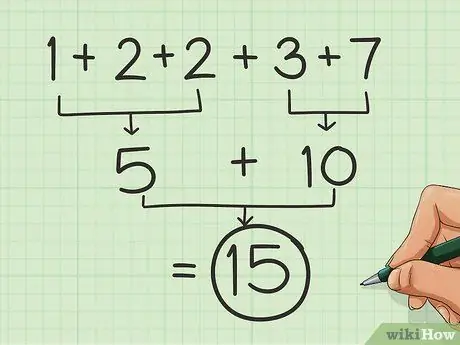
Step 2. Break it down into groups of round numbers
Similarly to the pairs of numbers analyzed in the first part, look for sets that give 5 or 10 (or 50, 100, 500 and 1000 etc.). Add the sets to make things easier.
So, for example: 7 + 1 + 2 = 10 and 2 + 3 = 5, so adding 1 + 2 + 2 + 3 + 7, you get 15
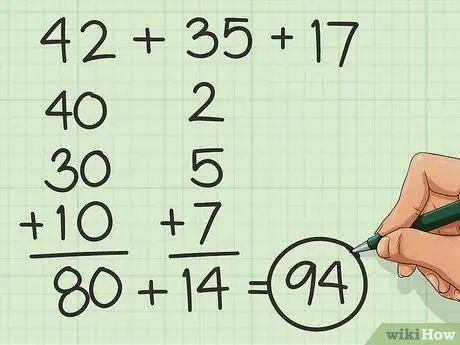
Step 3. Add to pieces
Break down units and tens to make numbers easier to count by adding up the tens and then just worrying about the units. For example, for some, it may be easier to add 40 + 30 + 10 and then 2 + 5 + 7, rather than 42 + 35 + 17.
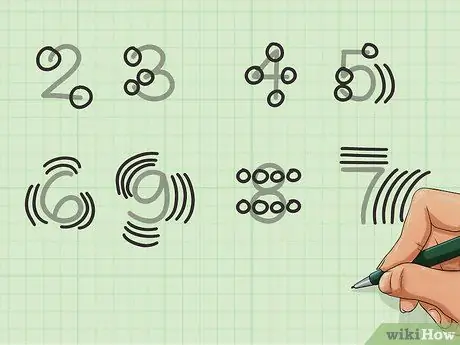
Step 4. Use the form of the number
If you just want to quickly sum in mind without using columns, and grouping methods don't suit you, you can use the form of numbers to count instead of relying on your fingers. It's easier if you only have a handful of numbers, anyway. For instance:
- The 2 has two ends. The 3 has three.
- The numbers 4 and 5 have their respective numbers of ends and conjunctions, with the curve of 5 valid as the conjunction.
- Certain numbers, such as 6, 7, 8 and 9 are less obvious. The curve of 6 and 9 is counted as three points (top, center and bottom) and is counted twice for 6 and three times for 9. Each side of each circle of 8 is counted as 1 (for a total of 4), which is doubled to get 8. The 7 is worth three points for the small upper part and four for the longer one.
Advice
- If the problem becomes so big that it is difficult to use the markings on the page (like 22 + 47), you will need more advanced addition methods.
- If the problem is small, and you think the answer is less than 10 (as in 2 + 5), you can do it without a pen and paper, and count with your fingers.
- When the student becomes familiar with this technique, you can show him that it is not necessary to count the first number from the beginning, but it is easier to start directly from that number. For example 8 + 2. Just make two signs, and count them starting from the other number … 8 … 9 … 10. In this way you can also add two numbers greater than 10 using your fingers, as long as the number to be added is less than or equal to 10.






